The Rectified 600-cell
The rectified 600-cell is a uniform polychoron bounded by 120 regular icosahedra and 600 octahedra. Since its cells are regular, it is also a semiregular polychoron. It has 720 cells, 720 vertices, 3600 edges, and 3600 triangles.

The dual of the rectified 600-cell is the joined 120-cell, one of the Catalan polychora.
Structure
The rectified 600-cell incorporates the structure of both the 120-cell and the 600-cell. Hence, we shall explore it using the same approach we use for the 120-cell and 600-cell: by means of its parallel projection.
First layer
We begin with the nearest icosahedral cell to the 4D viewpoint. We shall call this the “north pole” cell. It lies at the center of the projection envelope:

Only edges that lie on the projection envelope and on the icosahedral cell are shown, in order to reduce visual clutter.
Second layer
The 20 triangular faces of the north pole cell are joined to 20 octahedral cells. The next image shows 6 of these cells:

The following image shows 7 more of these cells:

The next image includes all 20 octahedral cells:

Third layer
There are 12 depressions into which another 12 icosahedra may be fitted. These icosahedra are shown in the next image:
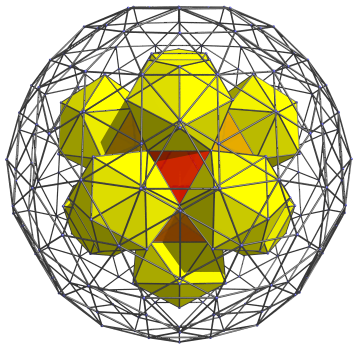
Next, the exposed triangular faces of the octahedral cells are joined to 20 more octahedra, shown in the next image:

Fourth layer
There are 30 more octahedra that may be fitted into depressions between each adjacent pair of icosahedra. These are shown below:

Next, there are 20 more icosahedral cells that are joined to the pink triangular faces, as shown below:
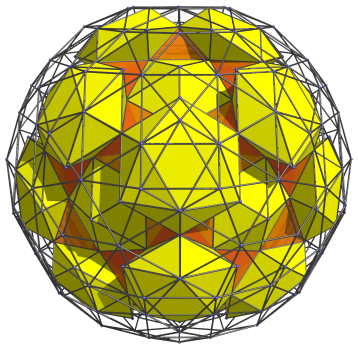
In the gaps between the orange octahedra and the icosahedra seen here, 60 more octahedra may be fitted in. These are shown next:

These octahedra form 12 circles of 5 octahedra each.
Fifth layer
Twelve more icosahedral cells fit nicely into each circle of 5 octahedra, as shown in the next image:

The remaining triangular faces of the 12 circles of 5 octahedra, seen here in red and orange, are joined to 60 more octahedral cells. These are shown next:

Sixth layer
Now between each pair of icosahedral cells, 60 more octahedra fit in, as shown below:

The remaining gaps, which are now clearly seen to be octahedral, fit the last 20 octahedral cells before we reach the equator. These are added in red below:

Equator
We have now reached the equator. The equator consists of 30 icosahedral cells and 60 octahedral cells. The 30 icosahedral cells are shown below. For clarity, we omit the northern hemisphere cells that we've seen so far.

These cells appear as flat hexagons because they lie in the hyperplane parallel to the camera's viewpoint. Notice how they straddle the octahedral cells in the previous image.
Finally, we show the 60 octahedral cells lying on the equator in the following image. They form 12 circles of 5 octahedra each.

Notice that there are triangular gaps here. These gaps are where the last 20 octahedral cells in the sixth layer, shown earlier in red, join with their corresponding counterparts in the southern hemisphere.
The Southern Hemisphere
From this point onwards, the arrangement of cells perfectly mirrors the structure of the northern hemisphere cells, in reverse order, until we reach the south pole icosahedral cell.
Summary
Counting the cells in each of the layers, we have:
Perspective Projection
Here's a perspective projection of the rectified 600-cell from a slightly different viewpoint:

The nearest icosahedral cell is shown in purple while the other icosahedral cells are shown in yellow; the octahedral cells are in transparent green.
Coordinates
The Cartesian coordinates of the rectified 600-cell, centered on the origin and having edge length 2, are all permutations of coordinates and all changes of sign of:
- (0, 0, 2φ, 2φ2)
- (1, 1, φ3, φ3)
along with all even permutations of coordinates and all changes of sign of:
- (0, 1, φ, 1+3φ)
- (0, φ2, φ3, 2+φ)
- (1, φ, 2φ2, φ2)
- (φ, φ2, 2φ, φ3)
where φ=(1+√5)/2 is the Golden Ratio.
Related Polychora
The high degree of symmetry of the rectified 600-cell masks very interesting subsymmetries within it; a particular CRF diminishing of it, the swirlprismatodiminished rectified 600-cell, exhibits a fascinating swirling substructure of 32 rings of cells that corresponds with the discrete partitioning of the Hopf fibration of the 4D sphere according to the structure of the icosidodecahedron.




