The Icosahedron
The regular icosahedron is one of the five Platonic solids. It is bounded by 20 equilateral triangles, and has 12 vertices and 30 edges. Its dual is the dodecahedron.

It can be cut into two pentagonal pyramids and a pentagonal antiprism, or a pentagonal pyramid and a gyroelongated pentagonal pyramid (J11). It can also be cut by two non-parallel planes to produce the metabidiminished icosahedron (J62), or by 3 planes to form the tridiminished icosahedron (J63).
Projections
In order to be able to identify the icosahedron in various projections of 4D objects, it is useful to know how it appears from various viewpoints. The following are some of the viewpoints that are commonly encountered:
| Projection | Envelope | Description |
|---|---|---|
 |
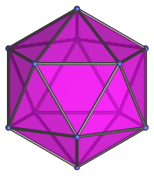
Regular decagon | Vertex-first parallel projection. |
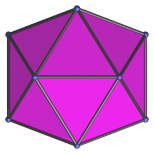 |
Hexagon | Edge-first parallel projection. Four of the icosahedron's faces project onto the top two and bottom two edges of the projection envelope. |
 |
Regular hexagon | Face-first parallel projection. |
 |
Non-uniform octagon | Parallel projection, parallel to two opposite faces. The two opposite faces project to the top and bottom edges of the projection envelope. |
Coordinates
The Cartesian coordinates of an origin-centered regular icosahedron of edge length 2 are:
- (0, ±1, ±φ)
- (±1, ±φ, 0)
- (±φ, 0, ±1)
where φ=(1+√5)/2 is the Golden Ratio.
Occurrences
The icosahedron occurs as cells in the following 4D uniform polytopes:
- The snub 24-cell;
- The truncated 600-cell;
- The rectified 600-cell.
In addition, it also occurs in many CRF polychora, including (but not limited to):




