The Octahedron

---

The regular octahedron is one of the Platonic solids. It is bounded by 8 equilateral triangles joined 4 to a vertex. It has 8 faces, 6 vertices, and 12 edges.

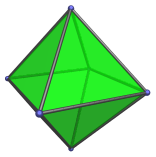
The dual of the octahedron is the cube. The octahedron occurs as cells in many 4D polytopes, most notably the regular 24-cell. The full list of occurrences is given below.

The octahedron can be bisected to form two square pyramids.

Projections

In order to be able to identify the octahedron in various projections of 4D objects, it is useful to know how it appears from various viewpoints. The following are some of the viewpoints that are commonly encountered:

Projection	Envelope	Description
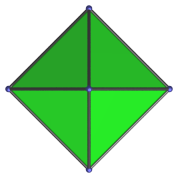	Square	Vertex-first parallel projection.
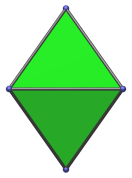	Rhombus	Edge-first parallel projection. Four of the faces project to the edges of the projection envelope.
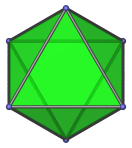	Hexagon	Face-first parallel projection.

Coordinates

The canonical coordinates of the regular octahedron are all permutations of:

• (±1,0,0)

These coordinates give an octahedron of edge length √2. An octahedron with edge length 2 has the coordinates:

• (±√2,0,0)

with all permutations of coordinates thereof.

Occurrences

The octahedron occurs as cells in many 4D polytopes, both regular and uniform:

• The 24-cell, a special 4D regular polytope;
• The rectified 5-cell, a uniform polychoron in the 5-cell family;
• The cantellated 5-cell;
• The cantellated tesseract;
• The truncated 16-cell;
• The runcinated 24-cell;
• The cantellated 120-cell;
• The rectified 600-cell.

Some CRF polychora also contain octahedral cells, including (but not limited to):

• Cube antiprism (K4.15) (aka octahedron antiprism);
• Octahedron atop rhombicuboctahedron (K4.107);
• The biparabigyrated cantellated tesseract;
• The tetrahedral ursachoron;
• The octahedral ursachoron;
• The octa-augmented runcitruncated 16-cell;
• The pentagonorhombic trisnub trisoctachoron (D4.11).