The Octahedral Ursachoron
The octahedral ursachoron is a CRF polychoron belonging to a family of polytopes that generalize the tridiminished icosahedron (J63) to higher dimensions. Its surface consists of 16 cells (1 octahedron, 8 tridiminished icosahedra (J63), 6 square pyramids, 1 cuboctahedron), 58 polygons (40 triangles, 6 squares, 12 pentagons), 66 edges, and 24 vertices.

It is the bigger brother of the tetrahedral ursachoron, having octahedral symmetry rather than tetrahedral.
Structure
We shall explore the structure of the octahedral ursachoron by means of its parallel projections into 3D.
Side-view
First, we shall look at the octahedral ursachoron from a side-view, centered on one of the edges encircled by 4 tridiminished icosahedra.
Near Side
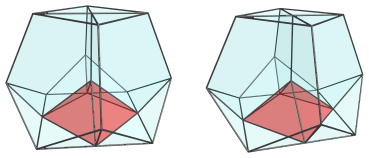
The above image shows one of the square pyramid cells that sit directly under the edge closest to the 4D viewpoint. It is somewhat foreshortened, because its base is actually slanting away into the 4th direction.
The next 4 images show each of the 4 tridiminished icosahedral cells that surround this edge, sitting above the square pyramid:
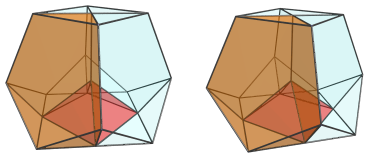
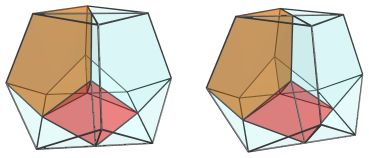
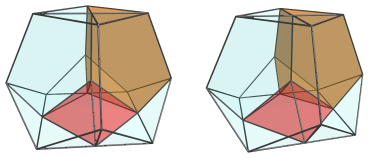
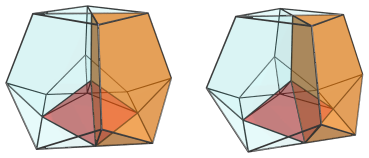
These cells appear squashed, due to perspective foreshortening, because they lie at an angle to the 4D viewpoint. In 4D, they are perfectly normal tridiminished icosahedra.
These are all the cells that lie on the near side of the polytope.
Equator
On the limb, or equator
of the polytope, there are 4 square pyramids,
shown below:
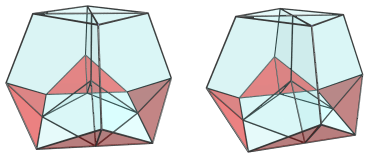
These square pyramids have been foreshortened into isosceles triangles, because they lie at a 90° angle to the 4D viewpoint. In 4D, they are perfectly normal square pyramids.
The top cell, an octahedron, also appears on the equator from the current 4D viewpoint:
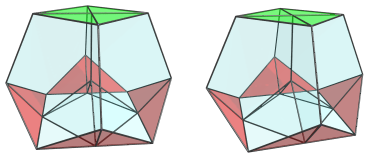
Like the square pyramids, this octahedron has been foreshortened into a square, due to its 90° angle to the 4D viewpoint.
The bottom cuboctahedron likewise:

The remaining pentagonal faces are not the projection images of any cell; they are where the 4 tridiminished icosahedra on the near side of the polychoron touch their 4 counterparts on the far side.
Summary
The arrangement of cells on the far side of the polytope mirror the arrangement of cells on the near side. Therefore, there are another 4 tridiminished icosahedra and a square pyramid on the far side. The following table summarizes the cell counts:
| Region | ||||
|---|---|---|---|---|
| Near side | 0 | 4 | 1 | 0 |
| Equator | 1 | 0 | 4 | 1 |
| Far side | 0 | 4 | 1 | 0 |
| Grand total | 1 | 8 | 6 | 1 |
| 16 cells | ||||
Top-view
The side-view projections of the octahedral ursachoron show its similarity to its tetrahedral analogue and the tridiminished icosahedron. However, its octahedral symmetry may not be immediately obvious. So now, we turn to its top-view projections: those centered on its octahedral cell.
Near side

This image shows the top octahedral cell. The octahedral symmetry of the entire polychoron is obvious from this viewpoint.
The faces of this octahedron are joined to 8 tridiminished icosahedra, shown below in 4 pairs:




The next image shows them all together:
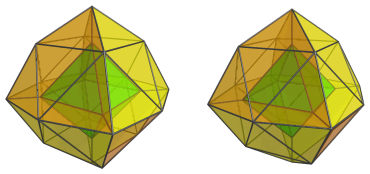
These tridiminished icosahedra appear quite squished along the direction of their 3-fold axis of symmetry, because of the angle they lie with respect to the 4D viewpoint.
Together with the octahedron, these are all the cells that lie on the near side of the polytope from this 4D viewpoint.
Far side
Now we come to the far side of the polychoron.

This image shows the cuboctahedral cell, which lies antipodal to the octahedron. Its square faces are joined to 6 square pyramids, shown below:

These cells are joined directly to the J63 cells of the near side; there are no equatorial cells from this 4D viewpoint.
Summary
The following table summarizes the cell counts from the top-down 4D viewpoint:
| Region | ||||
|---|---|---|---|---|
| Near side | 1 | 8 | 0 | 0 |
| Far side | 0 | 0 | 6 | 1 |
| Grand total | 1 | 8 | 6 | 1 |
| 16 cells | ||||
Coordinates
The Cartesian coordinates of the octahedral ursachoron with edge length 2 are:
- (±√2, 0, 0, √(2φ))
- (0, ±√2, 0, √(2φ))
- (0, 0, ±√2, √(2φ))
- (±φ√2, 0, 0, 0)
- (0, ±φ√2, 0, 0)
- (0, 0, ±φ√2, 0)
- (0, ±√2, ±√2, −√(2/φ))
- (±√2, 0, ±√2, −√(2/φ))
- (±√2, ±√2, 0, −√(2/φ))
where φ=(1+√5)/2 is the Golden Ratio.
Like the tetrahedral ursachoron, the octahedral ursachoron's vertices come in 3 sets, each lying on a parallel hyperplane: the vertices of an octahedron, a φ-scaled octahedron, and a cuboctahedron (rectified octahedron). The hyperplanes are suitably positioned so that regular pentagons are formed between the vertex layers. This follows the same pattern as the construction of a tridiminished icosahedron (J63): a triangle, a φ-scaled triangle, and a dual triangle (rectified triangle).
This construction is general, and applies to all dimensions, consisting of a base shape B, a φ-scaled copy of B, and a rectified version of B in parallel hyperplanes. In 2D, it yields the regular pentagon. In 3D, using an equilateral triangle as a base shape, it yields J63. It is possible to use a square as a base shape in 3D instead; the result is a direct lower-dimensional equivalent of the octahedral ursachoron, the square ursahedron. However, the square ursahedron is not CRF (it contains isosceles triangles with a base of length √2), and thus does not belong to the set of Johnson solids.
In 4D, the octahedral ursachoron is CRF. It is also possible to construct a cubical ursachoron, but it contains square ursahedra as cells and is thus non-CRF. In general, if the base shape of the construction is a regular (n-1)-dimensional polytope that whose 2D faces are all triangles, then the corresponding ursatope will contain CRF cells. The ursatope itself will be CRF provided it is convex and full-dimensioned. Specifically, the n-simplex ursatope exists and is CRF in all dimensions.
In 4D, there are 3 CRF ursachora:
- The tetrahedral ursachoron;
- the octahedral ursachoron (this page);
- and the icosahedral ursachoron, which happens to be a diminishing of the 600-cell.
Other ursachora are possible, but they are non-CRF.




