The Tetrahedral Ursachoron
The tetrahedral ursachoron is a CRF polychoron belonging to a family of polytopes that generalize the tridiminished icosahedron (J63) to higher dimensions. Its surface consists of 10 cells (5 tetrahedra, 4 tridiminished icosahedra, 1 octahedron), 30 polygons (24 triangles, 6 pentagons), 34 edges, and 14 vertices.
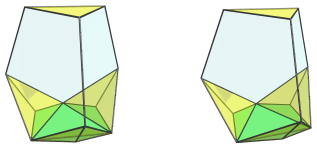
Structure
We shall explore the structure of the tetrahedral ursachoron by means of its parallel projections into 3D.
Side-view
First, we shall look at the tetrahedral ursachoron from a side-view, centered on one of its tridiminished icosahedral cells.
This image shows the nearest cell to the 4D viewpoint, a tridiminished icosahedron (J63).
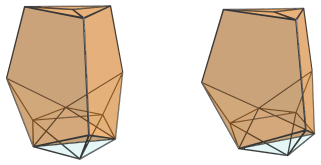
The next image shows 4 of its tetrahedral cells that are also visible from this viewpoint.
The top tetrahedron has been foreshortened into a triangle, because it lies perpendicular to the 4D viewpoint. Similarly, the 3 lower tetrahedra appear to be squished into narrow wedges. In 4D, however, they are perfectly regular tetrahedra.
The next image shows the octahedral cell that lies at the bottom of the polytope:
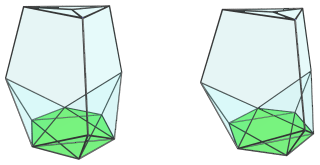
It appears foreshortened into a hexagon, because it also lies perpendicular to the 4D viewpoint. However, it is a perfectly regular octahedron in 4D.
These are all the cells that are visible from this 4D viewpoint. The top
tetrahedron and the bottom octahedron lie on the equator
, or limb, of
the polychoron; the tridiminished icosahedron and the other tetrahedra lie on
the near side.
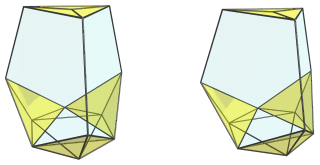
The remaining cells lie on the far side of the polytope. The following image shows the last tetrahedron, on the far side:
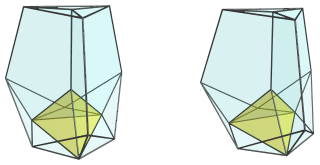
The remaining cells are 3 tridiminished icosahedra that sit around the central vertical edge in the projection image. For ease of reference, we leave the tetrahedron visible as well.
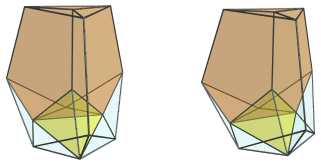
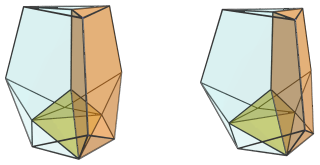
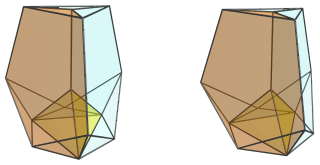
These tridiminished icosahedra look quite squished because they are at a steep angle relative to the 4D viewpoint. In 4D, they are perfectly normal tridiminished icosahedra.
These are all the cells that lie on the far side of the tetrahedral ursachoron. The following table summarizes the cell counts:
| Region | |||
|---|---|---|---|
| Near side | 3 | 1 | 0 |
| Equator | 1 | 0 | 1 |
| Far side | 1 | 3 | 0 |
| Grand total | 5 | 4 | 1 |
Top-view
The side-view projections of the tetrahedral ursachoron show its
upright
position, which shows its resemblance to the 3D tridiminished
icosahedron (J63). However, its inherent tetrahedral symmetry is not so obvious in
these projections. Therefore, we shall now look at its projections centered on
the top tetrahedral cell:

This image shows the nearest cell to the 4D viewpoint, which is the top tetrahedron. The resemblance to J63 is not so clear now, but the tetrahedral symmetry is obvious.
Next, we show the 4 J63 cells that are attached to each face of this top tetrahedron:
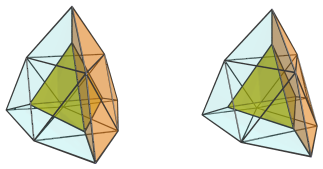

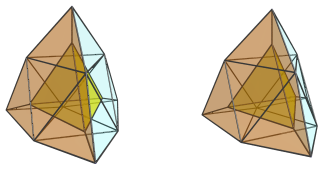
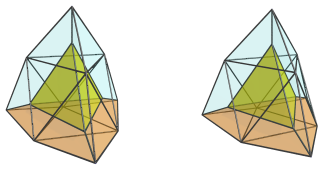
For reference, we have left the top tetrahedron visible in the above images.
These tridiminished icosahedra look quite squished because they lie at a pretty steep angle relative to the 4D viewpoint. They are, of course, perfectly normal tridiminished icosahedra in 4D.
These are all the cells that lie on the near side of the polytope from this 4D viewpoint. Now we come to the far side.
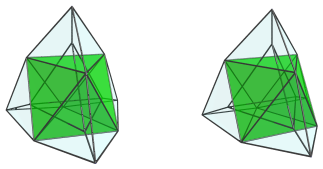
This image shows the octahedral cell, which lies antipodal to the top tetrahedron.
The following images show the remaining 4 tetrahedra:


The last image shows these tetrahedra together with the octahedron:
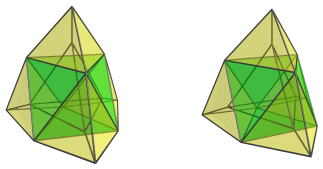
These are all the cells that lie on the far side of the polytope.
The following table summarizes the cell counts of the tetrahedral ursachoron from this 4D viewpoint:
| Region | |||
|---|---|---|---|
| Near side | 1 | 4 | 0 |
| Far side | 4 | 0 | 1 |
| Grand total | 5 | 4 | 1 |
Coordinates
The Cartesian coordinates of the tetrahedral ursachoron with edge length 2√2 are:
- ( 1, 1, 1, φ2)
- ( 1, -1, -1, φ2)
- (-1, 1, -1, φ2)
- (-1, -1, 1, φ2)
- ( φ, φ, φ, 0)
- ( φ, -φ, -φ, 0)
- (-φ, φ, -φ, 0)
- (-φ, -φ, φ, 0)
- (±2, 0, 0, -φ)
- ( 0, ±2, 0, -φ)
- ( 0, 0, ±2, -φ)
where φ=(1+√5)/2 is the Golden Ratio.
These coordinates come in three layers, corresponding respectively with the
vertices of a unit tetrahedron, a tetrahedron scaled by the Golden Ratio, and a
unit octahedron, with each layer spaced such that all edges are equal length.
The unit octahedron may be considered as a rectified tetrahedron
,
i. e., the convex hull of the midpoints of a tetrahedron's edges, rescaled
to unit edge length.
This is directly analogous to the construction of the vertices of the
tridiminished icosahedron in three layers, as a unit equilateral triangle, a
triangle scaled by the Golden Ratio, and a dual triangle (a rectified
triangle
).
This construction is, in fact, general across all dimensions: the convex hull of an n-simplex, a φ-scaled n-simplex, and a rectified n-simplex, placed in parallel hyperplanes spaced such that all edge lengths are equal. In 2D, the 1-simplex is just a unit edge, and the rectified edge is just a point. Thus, the construction yields a pentagon. In 3D, as already mentioned, the construction yields a tridiminished icosahedron. In 4D, the tetrahedral ursachoron is the result. In 5D, a corresponding ursateron is produced, and similarly in higher dimensions. Collectively, this construction yields the so-called ursatopes.
The name ursatope
is a wordplay on the Bowers Acronym for the
tridiminished icosahedron, teddi
,
punned as teddy
, a bear, which in Latin is ursula, from which
the shortened prefix ursa- is derived.




