The Cube Antiprism
The cube antiprism, or octahedron antiprism, also known as Octahedron atop Cube (octahedron || cube) or K4.15, is one of Richard Klitzing's convex segmentochora, 4D CRF polytopes whose vertices lie on two parallel hyperplanes and which are orbiform (can be inscribed into a 4D sphere).
Its surface consists of an octahedron and a cube in parallel hyperplanes, connected to each other by 6 square pyramids and 20 tetrahedra, for a total of 28 cells, 62 polygons (56 triangles, 6 squares), 48 edges, and 14 vertices.

Its name stems from one of the ways to generalize the 3D antiprisms to higher dimensions, namely, by considering the top and bottom faces of the antiprism not as rotated versions of each other, but as dual polygons to each other. The lacing triangles can then be analysed as "line segment pyramids". The 4D equivalent analogue of this construction, therefore, places a polyhedron and its dual, in this case the cube and octahedron, in two parallel planes, and connects the faces of one polyhedron with the vertices of the other with pyramids (in this case, square pyramids and tetrahedra as triangular pyramids), with tetrahedra connecting the edges of the respective polyhedra.
Structure
We shall explore the structure of the cube antiprism using its parallel projections into 3D, centered on its cubical cell.

For clarity, the above image shows only the cube, and render the remaining cells in a light transparent color.
The square faces of this cube are connected to 6 square pyramids, as shown in the next image:



The apices of these square pyramids touch the vertices of the octahedral cell, which is shown next:
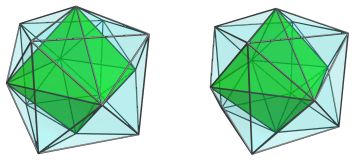
For clarity, we omit the cube and leave only the edge outlines of the square pyramid cells visible.
The faces of the octahedron are connected to 8 tetrahedra:


Between these 8 tetrahedra are 12 other tetrahedra, that connect the edges of the octahedron to the edges of the cube:

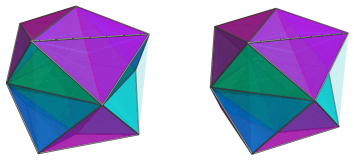

These are all the cells in the cube antiprism. The following table summarizes the cell counts:
| Layer | ||||
|---|---|---|---|---|
| 1 | 1 | 6 | 0 | 0 |
| 2 | 0 | 0 | 12 | 0 |
| 3 | 0 | 0 | 8 | 1 |
| Grand total | 1 | 6 | 20 | 1 |
| 28 cells | ||||
Coordinates
The Cartesian coordinates of K4.15, with edge length 2, are:
- (±√2, 0, 0, √(2√2−1))
- (0, ±√2, 0, √(2√2−1))
- (0,0, ±√2, √(2√2−1))
- (±1, ±1, ±1, 0)




