Cuboctahedron atop Truncated Cube
Cuboctahedron atop Truncated Cube (cuboctahedron || cube), or K4.129 among Dr. Richard Klitzing's segmentochora, is a 4D CRF polytope that consists of a cuboctahedron and a truncated cube in parallel hyperplanes, connected to each other by 8 triangular prisms and 6 square cupolae. It has a total of 16 cells, 64 polygons (28 triangles, 30 squares, 6 octagons), 84 edges, and 36 vertices.
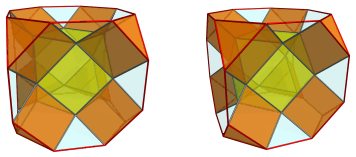
Besides the defining construction of taking the convex hull of a cuboctahedron and a truncated cube placed in parallel hyperplanes, K4.129 can also be constructed as a Stott expansion of the cubical pyramid (a cantellation).
Eight copies of K4.129 can be attached to the truncated tesseract to form the octa-augmented truncated tesseract, in which adjacent square cupolae lie in coincident hyperplanes and thus merge into square orthobicupolae (J28).
Structure
The structure of K4.129 is quite simple. We shall explore it using its parallel projections into 3D:
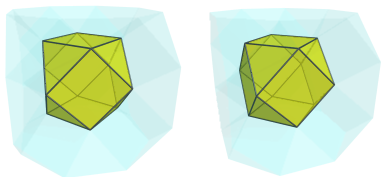
The above image shows the cuboctahedral cell. Its triangular faces are joined to 8 prisms, shown next:
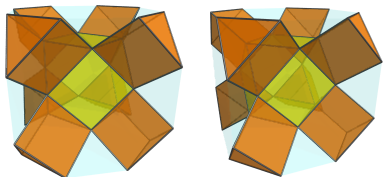
The square faces of the cuboctahedron are joined to 6 square cupolae:
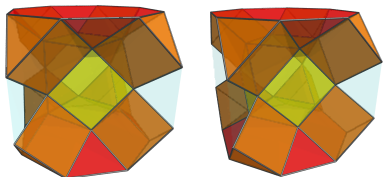
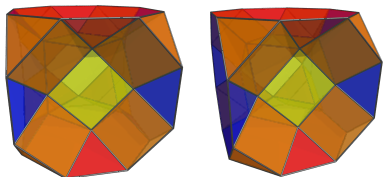
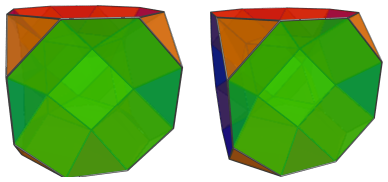
Finally, closing up the entire shape is the truncated cube:

For clarity, we show only the truncated cube and omit the cells previously seen.
Coordinates
The Cartesian coordinates of K4.129 with edge length 2 are:
- (0, ±√2, ±√2, 1)
- (±√2, 0, ±√2, 1)
- (±√2, ±√2, 0, 1)
- (±1, ±(1+√2), ±(1+√2), 0)
- (±(1+√2), ±1, ±(1+√2), 0)
- (±(1+√2), ±(1+√2), ±1, 0)




