Octahedron atop Rhombicuboctahedron
Octahedron atop rhombicuboctahedron (octahedron || rhombicuboctahedron), or K4.107 among Dr. Richard Klitzing's segmentochora, is a 4D CRF polytope that consists of an octahedron and a rhombicuboctahedron in parallel hyperplanes, connected to each other by 20 triangular prisms and 6 square pyramids, for a total of 28 cells, 82 polygons (40 triangles, 42 squares), 84 edges, and 30 vertices.
Eight copies of K4.107 can be attached to the runcitruncated 16-cell to form the octa-augmented runcitruncated 16-cell, in which the square pyramids of K4.107 and the cubes of the runcitruncated 16-cell lie in coincident hyperplanes and thus merge into elongated square bipyramids (J15).
Structure
The structure of K4.107 is quite simple. We shall explore it using its parallel projections into 3D:

The above image shows the octahedral cell of K4.107. It lies closest to this 4D viewpoint.
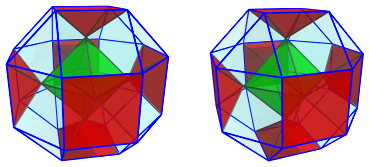
The next image shows 8 of the triangular prisms that are attached to this octahedron:
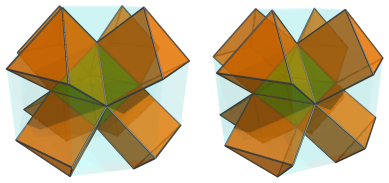
Between these triangular prisms are more triangular prisms, another 12 of them:
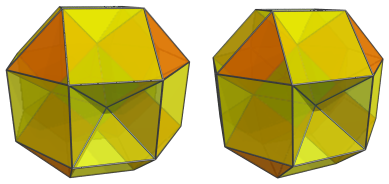
The remaining gaps are filled by 6 square pyramids:
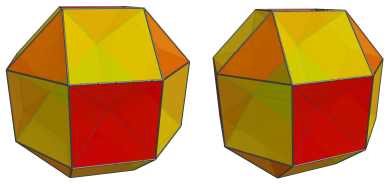
Finally, the last cell is the antipodal rhombicuboctahedron:
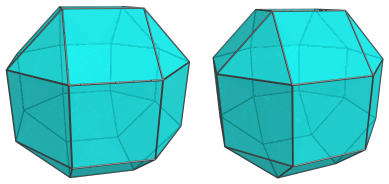
For clarity, we have omitted the other cells that have already been shown.
Coordinates
The Cartesian coordinates of K4.107 with edge length 2 are:
- (0, 0, ±√2, 1)
- (0, ±√2, 0, 1)
- (±√2, 0, 0, 1)
- (±1, ±1, ±(1+√2), 0)
- (±1, ±(1+√2), ±1, 0)
- (±(1+√2), ±1, ±1, 0)




