The Icosidodecahedron

---

The icosidodecahedron is a uniform polyhedron bounded by 32 polygons (12 pentagons and 20 triangles), 60 edges, and 30 vertices. It is edge-uniform, and its two kinds of faces alternate around each vertex, so it is also a quasi-regular polyhedron. It may be constructed by truncating the dodecahedron or the icosahedron at the midpoints of its edges.

The dual of the icosidodecahedron is the rhombic triacontahedron, a Catalan solid.

The icosidodecahedron may be bisected along one of its decagonal circuits of edges to yield two pentagonal rotundae (J6), one of the Johnson solids:

Inserting a decagonal prism between the two rotundae produces an elongated pentagonal gyrobirotunda (J43).

Pasting the two rotundae together in wrong orientation (ortho orientation) produces the pentagonal orthobirotunda (J34), another Johnson solid.

The icosidodecahedron may also be bisected with a plane parallel to two opposite triangles; in this case, the result will no longer have regular faces. However, it can be modified to have regular faces by shrinking the six vertices that lie on the bisecting plane towards the center by the Golden Ratio. This modified bisection produces two triangular hebesphenorotundae (J92), another of the Johnson solids:

Projections

In order to be able to identify the icosidodecahedron in various projections of 4D objects, it is useful to know how it appears from various viewpoints. The following are some of the commonly-encountered views:

Projection	Envelope	Description
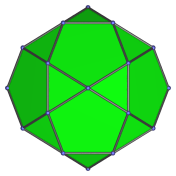
	Decagon	Parallel projection centered on a pentagonal face.
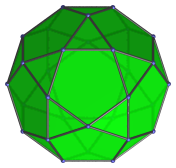
	Dodecagon	Parallel projection centered on a triangular face.
	Non-uniform octagon	Vertex-centered parallel projection. The edges of the projection envelope are images of 4 pentagons (the longer edges) and 4 triangles (the shorter edges).
	Non-uniform decagon	Edge-centered projection. The top and bottom edges of the projection envelope are the images of two pentagonal faces.

Coordinates

The Cartesian coordinates of the icosidodecahedron, centered on the origin and having edge length 2, are all permutations of coordinates of:

• (0, 0, ±2φ)

together with the even permutations of coordinates of:

• (±1, ±φ², ±φ)

where φ=(1+√5)/2 is the Golden Ratio.

It is evident from the first set of coordinates that an octahedron can be inscribed in an icosidodecahedron.

Occurrences

The icosidodecahedron occurs as cells in two uniform polychora: the rectified 120-cell and the cantellated 600-cell.