The Rhombic Triacontahedron

---

The rhombic triacontahedron is a 3D Catalan solid bounded by 30 rhombuses, 60 edges, and 32 vertices. It is the dual of the icosidodecahedron.

The faces are transitive, each a rhombus with a diagonal ratio of 1 : φ, where φ=(1+√5)/2 is the Golden Ratio. Unlike most of the other Catalan solids, the edges are also transitive, due to the icosidodecahedron being quasi-regular.

The 32 vertices are of two kinds: 20 vertices where 5 edges meet, corresponding to an inscribed icosahedron, and 12 vertices where 3 edges meet, corresponding to an inscribed dodecahedron.

The rhombic triacontahedron is one of the projection envelopes of the castellated rhombicosidodecahedral prism, a CRF polychoron that has bilunabirotunda cells. In this projection, each rhombus is the projection image of a bilunabirotunda, each order 3 vertex corresponds with a tetrahedron, and each order 5 vertex corresponds with a pentagonal prism.

Projections

The following are images of the rhombic triacontahedron from various viewpoints:

Projection	Description
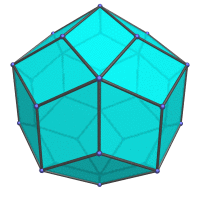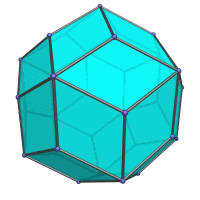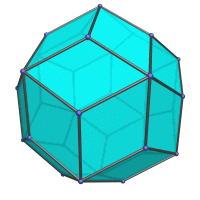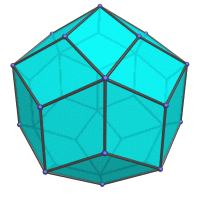
	Projection centered on an order-5 vertex.
	Centered on an order-3 vertex.
	Centered on a face.
	Centered on an edge.

Animation

Here's an animation of a rhombic triacontahedron rotating around the vertical axis:

Coordinates

The Cartesian coordinates for the rhombic triacontahedron are all permutations of coordinate and all changes of sign of:

• (φ, φ, φ)

along with even permutations of coordinate and all changes of sign of:

• (0, φ², 1)
• (0, φ, φ²)

where φ=(1+√5)/2 is the Golden Ratio.

These coordinates are obtained by inverting an icosidodecahedron of edge length 1/φ³.