The Pentagonal Icositetrahedron

---

The pentagonal icositetrahedron is a 3D Catalan solid bounded by 24 non-regular pentagons, 60 edges (36 short, 24 long), and 38 vertices. It is the dual of the snub cube.

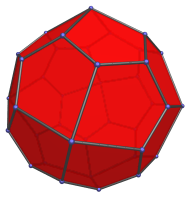
The pentagonal faces are transitive, with 3 short edges opposite 2 long edges that meet at an apical vertex. The ratio of short to long edge lengths is 2/(τ+1) : 1, or approximately 0.704 : 1, where τ is the so-called tribonacci constant, the unique real root of the polynomial:

τ³ − τ² − τ − 1 = 0

Numerically, τ ≈ 1.839286755214161.

Each pentagon has mirror symmetry across the line that stretches from the apex to the midpoint of the opposite short edge.

The chord between the two ends of the long edges is exactly τ times the length of a short edge. In the above image, this chord is the horizontal distance between the two vertices in the middle of the pentagon, between the top and bottom vertices.

The 38 vertices are of three kinds: 6 apical vertices where 4 long edges meet, 8 corner vertices where 3 short edges meet, and 24 lateral vertices where one long edge and two short edges meet.

Like the snub cube, the pentagonal icositetrahedron is chiral: it is distinct from its mirror-image. Its two forms are its enantiomorphs, shown below:

Projections

The following are images of the pentagonal icositetrahedron from various viewpoints:

Projection	Description
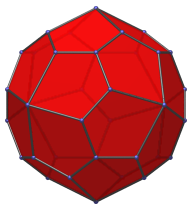
	Front view, centered on an axial vertex.
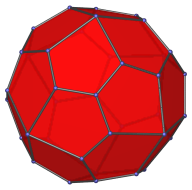
	Side view, centered on an edge between two lateral vertices.
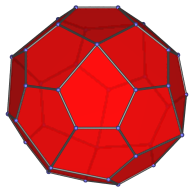
	Octant view, centered on a corner vertex.
	Face-first projection.

Animation

Here's an animation of a pentagonal icositetrahedron rotating around the vertical axis:

Coordinates

The Cartesian coordinates for the pentagonal icositetrahedron are all permutations of coordinate and changes of sign of:

• (0, 0, τ³)
• (τ², τ², τ²)

along with even permutations of coordinate and even changes of sign of:

• (1, τ², −(2τ+1))
• (1, 2τ+1, τ²)

where τ is the tribonacci constant, the unique positive root of:

τ³ − τ² − τ − 1 = 0

The coordinates of the enantiomer (mirror image) of the pentagonal icositetrahedron are the same as the above, except that odd permutations of coordinate are taken for the second set of coordinates instead of even permutations.

These coordinates are obtained by inverting a snub cube of edge length √(20τ − 2τ² − 30), or approximately 0.140654073779424.

Credits

The coordinates were obtained from the Wikipedia page on the pentagonal icositetrahedron and independently verified.