The Triakis Icosahedron
The triakis icosahedron is a 3D Catalan solid bounded by 60 isosceles triangles, 90 edges (60 short and 30 long), and 32 vertices. It is the dual of the truncated dodecahedron.

The faces are transitive isosceles triangles with 2 short edges and 1 long edge. The edge length ratio is (8−φ)/11 : 1 (approximately 0.580 : 1), where φ=(1+√5)/2 is the Golden Ratio.
The 32 vertices are of two kinds: 20 vertices where 3 short edges meet, corresponding to an inscribed icosahedron, and 12 vertices where 10 edges meet (5 long, 5 short), corresponding to an inscribed dodecahedron.
Projections
The following are images of the triakis icosahedron from various viewpoints:
| Projection | Description |
|---|---|
 |
Projection centered on an order-10 vertex. |
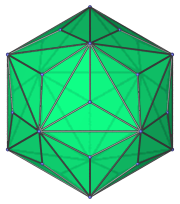 |
Centered on an order-3 vertex. |
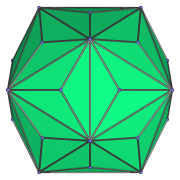 |
Centered on a long edge. |
 |
Centered on a short edge. |
Animation
Here's an animation of a triakis icosahedron rotating around the vertical axis:

Coordinates
The Cartesian coordinates for the triakis icosahedron are all changes of sign of:
- (1, 1, 1)
along with even permutations of coordinate and all changes of sign of:
- (0, φ, 1/φ)
- (0, (7φ−6)/5, (φ+7)/5)
where φ=(1+√5)/2 is the Golden Ratio.
The edge length of the corresponding dual truncated icosahedron is (10φ−14)/11.




