The Triakis Tetrahedron

---

The triakis tetrahedron is a 3D Catalan solid bounded by 12 isosceles triangles, 18 edges (6 long edges, 12 short edges), and 8 vertices. It is the dual of the truncated tetrahedron.

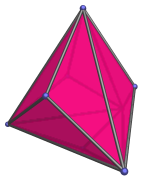
The triakis in the name means to erect pyramids on triangular faces; triakis tetrahedron means the polyhedron obtained by erecting pyramids on the triangular faces of the regular tetrahedron.

The triangular faces are transitive, consisting of 2 short edges and 1 long edge, with a 3 : 5 length ratio. The 8 vertices are of two kinds: 4 order-6 vertices corresponding to an inscribed tetrahedron, and 4 order-3 vertices corresponding to the apices of the triangular pyramids erected on this inscribed tetrahedron.

The triakis tetrahedron is the envelope of the vertex-first projection of the joined pentachoron, a 4D Catalan polychoron, into 3D.

Projections

The following are images of the triakis tetrahedron from various viewpoints:

Projection	Description
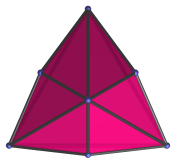	Parallel projection centered on top vertex.
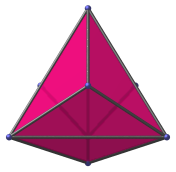	Side view looking at vertex with short edges.
	Front view looking at long edge.
	Oblique side view with many coinciding edges.

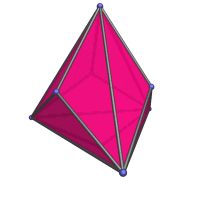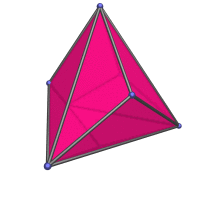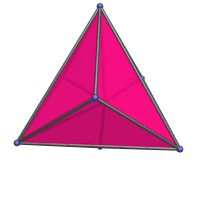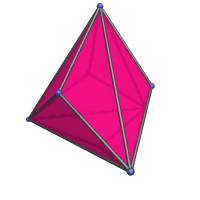
Animation

Here's an animation of a triakis tetrahedron rotating around the vertical axis:

Coordinates

The Cartesian coordinates for the triakis tetrahedron, obtained by inverting a truncated tetrahedron centered on the origin with edge length 2, are:

• (2/√6, 0, 0)
• (−6/(5√6), 0, 0)
• (2/(5√6), −4/(5√3), 0)
• (−2/(3√6), 4/(3√3), 0)
• (2/(5√6), 2/(5√3), ±2/5)
• (−2/(3√6), −2/(3√3), ±2/3)

These coordinates give an “upright” triakis tetrahedron, in the sense that the inscribed tetrahedron outlined by its long edges has one face parallel to the horizon.

Algebraically nicer coordinates may be obtained in a different orientation by constructing the triakis tetrahedron from the truncated tetrahedron as the truncated alternation of the cube. The resulting coordinates are all even changes of sign of:

• (1, 1, −1)
• (5/3, 5/3, 5/3)

Credits

The coordinates derived from the truncated alternation of the cube are obtained from the Wikipedia article on the triakis tetrahedron.