The Rhombic Dodecahedron
The rhombic dodecahedron is a 3D Catalan solid bounded by 12 rhombuses, 24 edges, and 14 vertices. It is the dual of the cuboctahedron.
The faces are transitive, each a rhombus with a diagonal ratio of 1 : √2. The adjective rhombic in the name refers these rhombuses, in order to distinguish it from the regular dodecahedron, which also has 12 faces, but which are regular pentagons rather than rhombuses.
Unlike most of the other Catalan solids, the edges of the rhombic dodecahedron are also transitive, due to the dual cuboctahedron being quasi-regular. The 14 vertices are of two kinds: 6 apical vertices corresponding to an inscribed octahedron, and 8 vertices corresponding to an inscribed cube.
The rhombic dodecahedron is the projection envelope of the tessarect and the 24-cell in their vertex-first parallel projections into 3D.
Projections
The following are images of the rhombic dodecahedron from various viewpoints:
| Projection | Description |
|---|---|
 |
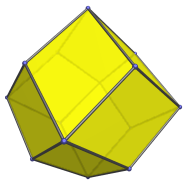
Front view, centered on an apical vertex. |
 |
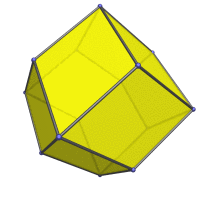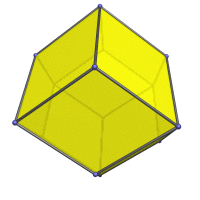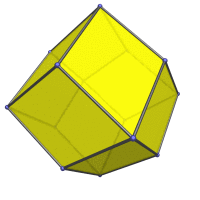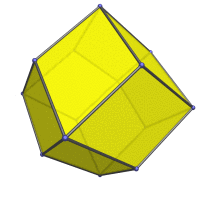
Centered on a face. |
 |
Centered on a cube vertex. From this viewpoint it appears to be the same as a cube. |
Animation
Here's an animation of a rhombic dodecahedron rotating around the vertical axis:
Coordinates
The Cartesian coordinates for the rhombic dodecahedron are all permutations of coordinate and changes of sign of:
- (0, 0, 2)
- (1, 1, 1)
The corresponding dual cuboctahedron has edge length 1/√2.
Properties
The rhombic dodecahedron can tile space: multiple copies of it can be stacked together in such a way that they fill up 3D space without any gaps.
Its 4D analogue is the 24-cell, which can also tile space. Unlike the 24-cell, however, the rhombic dodecahedron is not regular: its rhombic faces are not regular polygons. Nevertheless, it is face-transitive and edge-transitive, just like the 24-cell.




