The Triakis Octahedron

---

The triakis octahedron is a 3D Catalan solid bounded by 24 isosceles triangles, 36 edges (24 short, 12 long), and 14 vertices. It is the dual of the truncated cube.

The faces are transitive; isosceles triangles with two short edges and a long edge with a (2−√2) : 1 length ratio, or approximately 0.586 : 1.

The 14 vertices are of three kinds: 6 axial vertices corresponding to an inscribed octahedron, and 8 vertices corresponding to an inscribed cube.

Projections

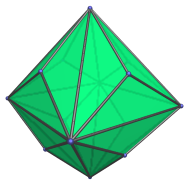
The following are images of the triakis octahedron from various viewpoints:

Projection	Description
	Front view, centered on axial vertex.
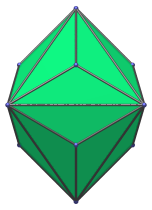	Side view, centered on a long edge.
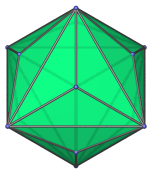	Octant view, centered on a cube vertex.

Animation

Here's an animation of a triakis octahedron rotating around the vertical axis:

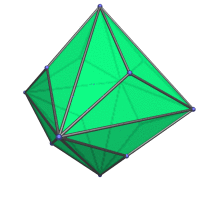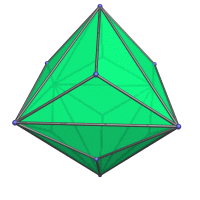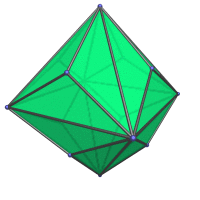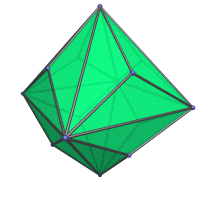
Coordinates

The Cartesian coordinates for the triakis octahedron are all permutations of coordinate and changes of sign of:

• (0, 0, 1+√2)
• (1, 1, 1)

These coordinates correspond with a dual truncated cube of edge length (6−4√2).