The Triangular Hebesphenorotunda
The triangular hebesphenorotunda is the 92nd and last Johnson solid (J92). Its surface consists of 20 faces (13 equilateral triangles, 3 squares, 3 regular pentagons, 1 regular hexagon), 36 edges, and 18 vertices.
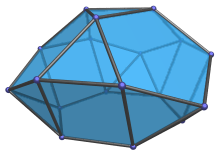
Structure
The triangular hebesphenorotunda is one of the special Johnson solids at the end of Norman Johnson's list that are not directly derived from the uniform polyhedra by cut-and-paste operations. Nevertheless, it is closely related to the icosidodecahedron. The top part of its surface, where 3 pentagons and 3 triangles surround a central triangle, is in fact part of the surface of an icosidodecahedron. Furthermore, its hexagonal face lies on the plane that bisects this icosidodecahedron.
The following diagram shows this relationship:
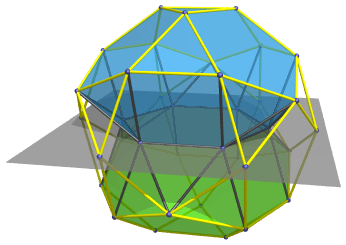
The green solid is a second triangular hebesphenorotunda, joined in gyro orientation to the first at the hexagonal face. The yellow edges show the outline of the icosidodecahedron that they are inscribed in, and the grey plane is the plane that bisects it.
As is evident, the hexagonal face lies on this plane. Six of the icosidodecahedron's vertices lie on this plane as well. In fact, they lie on the vertices of a hexagon that is simply this hexagonal face scaled by the Golden Ratio φ=(1+√5)/2.
In other words, the triangular hebesphenorotunda may be thought of as an icosidodecahedron bisected with a plane parallel to two opposite triangular faces, with the 6 vertices that lie on the bisecting plane shrunk down towards its center by the Golden Ratio so that all edges become unit length.
Projections
In order to be able to identify the triangular hebesphenorotunda in various projections of 4D objects, it is useful to know how it appears from various viewpoints. The following are some of the viewpoints that are commonly encountered:
| Projection | Envelope | Description |
|---|---|---|
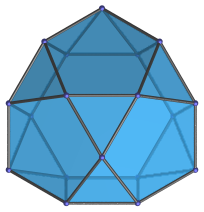 |
Irregular nonagon | Parallel projection along axis of symmetry. |
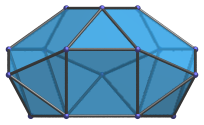 |
Irregular octagon | Projection parallel to a pair of opposite edges of the hexagonal face. |
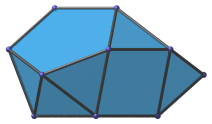 |
Irregular hexagon | Projection with the most coincident elements, parallel to a pair of opposite vertices of the hexagonal face. The top, upper left, and lower right edges are images of triangles; the upper right edge is the image of a pentagon; the bottom edge the image of the hexagon. All apparent faces are the images of pairs of faces of that respective shape. |
Coordinates
The Cartesian coordinates of the triangular hebesphenorotunda are:
|
|
where φ=(1+√5)/2 is the Golden Ratio. These coordinates give a triangular hebesphenorotunda with edge length 2, with its axis of symmetry aligned with the Z axis and its hexagonal face on the XY plane.
Occurrences
In spite of its seemingly irregular shape, its deep connection to the icosahedron allows the triangular hebesphenorotunda to appear as cells in a good number of CRF polychora, generalizations of the Johnson solids to 4D, including (but not limited to):




