The Pentagonal Gyrocupolarotunda

---

The pentagonal gyrocupolarotunda is the 33rd Johnson solid (J33). It has 25 vertices, 50 edges, and 27 faces (15 equilateral triangles, 5 squares, and 7 pentagons).

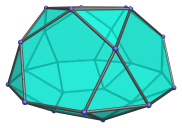
The pentagonal gyrocupolarotunda can be constructed by joining a pentagonal rotunda to a pentagonal cupola at their decagonal face, such that the pentagonal faces of the rotunda share edges with the square faces of the cupola. The gyro- in the name refers to how the orientation of the top and bottom pentagons are rotated with respect to each other. Joining the cupola and rotunda in ortho orientation produces the pentagonal orthocupolarotunda (J32) instead.

Projections

Here are some views of the pentagonal gyrocupolarotunda from various angles:

Projection	Description
	Top view.
	Front view.
	Side view.

Coordinates

The Cartesian coordinates of the pentagonal gyrocupolarotunda with edge length 2 are:

• (−√((10+2√5)/5), 0, √((20+8√5)/5))
• (−√((5−√5)/10), ±φ, √((20+8√5)/5))
• ( √((5+2√5)/5), ±1, √((20+8√5)/5))
• ( √((20+8√5)/5), 0, √((10+2√5)/5))
• (−√((25+11√5)/10), ±φ, √((10+2√5)/5))
• ( √((5+√5)/10), ±φ², √((10+2√5)/5))
• (±√(3+4φ), ±1, 0)
• (±√(2+φ), ±φ², 0)
• (0, ±2φ, 0)
• (√((10+2√5)/5), 0, −2√((3−φ)/5))
• (√((5−√5)/10), ±φ, −2√((3−φ)/5))
• (−√((5+2√5)/5), ±1, −2√((3−φ)/5))

where φ = (1+√5)/2 is the Golden Ratio, approximately 1.61803.