The Hebe­spheno­mega­corona

---

The hebesphenomegacorona is the 89th Johnson solid (J89). Its surface consists of 21 regular polygons (18 triangles and 3 squares), 33 edges, and 14 vertices.

The hebesphenomegacorona is one of the special Johnson solids at the end of Norman Johnson's list that are not directly derived from the uniform polyhedra by cut-and-paste operations. As Norman Johnson explains, a lune is a square with two opposite edges attached to equilateral triangles, and a spheno (Latin for wedge) complex is two lunes joined together to form a wedge-like structure. A hebespheno complex is a larger, blunter complex of three lunes. A corona is a crown-like complex of 8 triangles, whereas a megacorona is a larger corona with 12 triangles. Hebespheno­megacorona, therefore, describes the structure built from a hebespheno complex attached to a megacorona of 12 triangles.

Projections

Here are some views of the hebesphenomegacorona from various angles:

Projection	Description
	Top view.
	Front view.
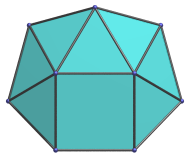	Side view.
	45° side view.

Coordinates

The Cartesian coordinates of the hebesphenomegacorona with edge length 2 are:

• (±1, ±1, 2B)
• (±1, ±(1+2A), 0)
• (±(1 + C/√(1−A)), 0, −(2A²+A−1)/B)
• (0, ±1, −D)
• (±(DC+E)/(FE), 0, ((2A−1)D)/F − C/(FE))

where:

• B = √(1−A²)
• C = √(2(1−2A))
• D = √(3−4A²)
• E = √(1+A)
• F = 2(1−A)

and A is the root of the following polynomial between 0.2 and 0.22:

26880A¹⁰ + 35328A⁹ − 25600A⁸ − 39680A⁷ + 6112A⁶ + 13696A⁵ + 2128A⁴ − 1808A³ − 1119A² + 494A − 47 = 0

The approximate value of A is 0.216844815713457.

Credits

The above coordinates were adapted from the solution published by A. V. Timofeenko (2008), The non-Platonic and non-Archimedean noncomposite polyhedra, Fundamentalnaya i Prikladnaya Matematika, vol.14 (2), pp.179-205. (А. В. Тимофеенко (2008) «Несоставные многогранники, отличные от тел Платона и Архимеда», Фундаментальная и Прикладная Математика, том 14-й (2), ст.179-205.)

An error in the printed coordinates of the last set of vertices in the paper was corrected: a factor of 2 in the denominator of the first term in the last coordinate was misprinted as 4, thus effectively turning ((2A−1)D)/F into ((2A−1)D)/(2F). This error appears to be a mere typo; the derivation itself is correct, and the correct coordinates can be derived from it. This correction was pointed out by Loïs Mignard.