The Triangular Orthobicupola
The triangular orthobicupola is the 27th Johnson solid (J27). It has 12 vertices, 24 edges, and 14 faces (8 equilateral triangles and 6 squares).

The triangular orthobicupola can be constructed by joining two triangular cupolae to each other at their hexagonal face, such that the square faces touch each other at the edges. The ortho in the name refers to how the orientation of the two cupolae line up with each other.
It can also be constructed by rotating half of a cuboctahedron by 60°, and thus could be regarded as a gyrated cuboctahedron. Conversely, the cuboctahedron could be considered as a triangular gyrobicupola.
The height of a triangular orthobicupola with edge length 2 is 4√(2/3), or approximately 3.265986.
Inserting a hexagonal prism between the two constituent triangular cupolae produces an elongated triangular bicupola, another Johnson solid.
Projections
Here are some views of the triangular orthobicupola from various angles:
| Projection | Description |
|---|---|
 |
Top view. |
 |
Front view. |
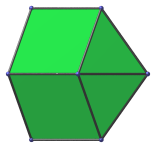 |
Side view, with many coincident edges. |
Coordinates
The Cartesian coordinates of the triangular orthobicupola with edge length 2 are:
- (±1, −1/√3, ±√(8/3))
- (0, 2/√3, ±√(8/3))
- (±1, ±√3, 0)
- (±2, 0, 0)




