The Pentagonal Rotunda
The pentagonal rotunda is the 6th Johnson solid (J6). Its surface consists of 10 equilateral triangles, 6 regular pentagons, and 1 regular decagon, for a total of 17 faces, 35 edges, and 20 vertices.
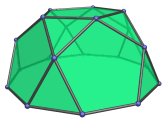
It can be constructed by bisecting the icosidodecahedron along one of its decagonal circuits of edges. Thus, it may be also called the bisected icosidodecahedron. Conversely, joining a pair of pentagonal rotundae in gyro orientation at their decagonal faces produces an icosidodecahedron:

Thus, the icosidodecahedron may also be named the pentagonal gyrobirotunda.
If the pentagonal rotundae are joined in ortho orientation instead, we obtain the pentagonal orthobirotunda (J34), another Johnson solid.

The pentagonal rotunda can also be elongated by attaching a decagonal prism to form an elongated pentagonal rotunda (J21), also a Johnson solid. Elongating with a decagonal antiprism instead produces a gyroelongated pentagonal rotunda (J25).
The pentagonal rotunda can also be attached to a pentagonal cupola, producing either a pentagonal orthocupolarotunda (J32) or a pentagonal gyrocupolarotunda (J33), depending on its orientation with respect to the cupola.
The cupolarotundae thus produced may also be elongated by the insertion of a decagonal prism, producing the elongated pentagonal orthocupolarotunda (J40) and the elongated pentagonal gyrocupolarotunda (J41), respectively.
If two rotundae are used instead of a rotunda and a cupola, the result is the elongated pentagonal orthobirotunda (J42) and the elongated pentagonal gyrobirotunda (J43) instead.
If a decagonal antiprism is used instead of the decagonal prism, we get either the gyroelongated pentagonal cupolarotunda (J47) or the gyroelongated pentagonal birotunda (J48), depending on whether a cupola or a rotunda is on the other side.
Projections
In order to be able to identify the pentagonal rotunda in various projections of 4D objects, it is useful to know how it appears from various viewpoints. The following are some of the viewpoints that are commonly encountered:
| Projection | Envelope | Description |
|---|---|---|
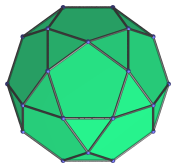 |
Regular decagon | Parallel projection centered on top pentagon. |
 |
Bisected decagon | Projection parallel to a pair of opposite edges of the decagonal face. |
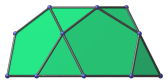 |
Bisected irregular octagon | Projection parallel to a pair of opposite vertices of the decagonal face. This projection has the largest number of coincident elements. |
Coordinates
The Cartesian coordinates of the pentagonal rotunda are:
|
|
| |
where φ = (1+√5)/2 is the Golden Ratio, A = √((10+2√5)/5), and B = √((5+2√5)/5).
These coordinates give a pentagonal rotunda of edge length 2 in a “nice” orientation, with its 5-fold axis of symmetry aligned to the Z axis and its decagonal face resting on the XY plane.
Algebraically “nicer” coordinates may be obtained by taking advantage of its relationship to the icosidodecahedron, by deleting 10 vertices from the latter. The coordinates thus obtained are:
| (0, 0, 2φ) | (0, 2φ, 0) | (±2φ, 0, 0) |
| (±1, ±φ, φ2) | (±1, φ, −φ2) | (±φ, φ2, ±1) |
| (±φ2, ±1, φ) | (±φ2, 1, −φ) |
These coordinates do not give a pentagonal rotunda in a “nice” orientation, but they are algebraically nicer because they can be simply expressed in terms of the Golden Ratio φ, and do not involve nested square roots.