The Icosagonal Prism
The icosagonal prism is a 3D uniform polyhedron bounded by 22 polygons (2 icosagons—20-sided polygons—and 20 squares), 60 edges, and 40 vertices. It may be considered the extrusion of the icosagon.
Projections
In order to be able to identify the icosagonal prism in various projections of 4D objects, it is useful to know how it appears from various viewpoints. The following are some of the commonly-encountered views:
| Projection | Description |
|---|---|
 |
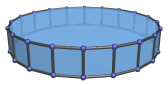
Centered on icosagon. |
 |
Centered on edge. |
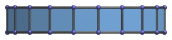 |
Centered on square. |
 |
Centered on vertex. |
Coordinates
The Cartesian coordinates of the icosagonal prism, centered on the origin and having edge length 2, are:
- (0, ±A, ±1)
- (±A, 0, ±1)
- (±B, ±C, ±1)
- (±C, ±B, ±1)
- (±D, ±E, ±1)
- (±E, ±D, ±1)
where:
| A | = | 2√(2φ2+√(11φ+7)) |
| B | = | √(2+√(φ+2)) |
| C | = | √(6+8φ+√(145φ+90)) |
| D | = | √(4+2φ+√(20φ+15)) |
| E | = | √(4+6φ+√(76φ+47)) |
| φ | = | (1+√5)/2 |
Numerically, they are approximately:
| A | = | 6.39245322149966 |
| B | = | 1.97537668119028 |
| C | = | 6.07958429141920 |
| D | = | 3.75738972956701 |
| E | = | 5.17160329194011 |
| φ | = | 1.61803398874989 |
Occurrences
The icosagonal prism occurs in the following uniform polychora:
- The 5,20-duoprism.
It also occurs in the following CRF polychora:




