The 5,20-Duoprism

---

The 5,20-duoprism is a 4D uniform polychoron in the infinite duoprism family. It is the Cartesian product of an icosagon (20-sided polygon) and a pentagon, and has a surface consisting of 25 cells (20 pentagonal prisms and 5 icosagonal prisms), 125 polygons (5 icosagons, 20 pentagons, and 100 squares), 200 edges, and 100 vertices.

The 5,20-duoprism can be augmented with pentagonal prism pyramids and remain convex, as long as the augments are separated by at least one intervening pentagonal prism. The dichoral angle between two adjacent pentagonal prisms, which is the internal angle of the regular icosagon, is exactly 162°; and the dichoral angle between the base pentagonal prism and a pentagonal pyramid cell in the pentagonal prism pyramid is exactly 18°. Thus, the pentagonal pyramid cells from an augment would merge with the adjacent pentagonal prisms from the duoprism to form elongated pentagonal pyramids (J9). If there is another augment on the other side of the intervening pentagonal prism, a second pentagonal pyramid cell would merge with the elongated pyramid to form an elongated pentagonal bipyramid (J16).

The maximal augmentation of the 5,20-duoprism with pentagonal prism pyramids is the deca-augmented 5,20-duoprism, where every other pentagonal prism is augmented, resulting in a polychoron that contains 10 elongated pentagonal bipyramids (J16).

Structure

Centered on an Icosagonal Prism

The structure of the 5,20-duoprism is relatively straightforward. It consists of two rings of prisms. The first ring consists 5 icosagonal prisms wrapped around in a pentagonal arrangement:

The second ring consists of 20 pentagonal prisms wrapped around in an icosagonal arrangement:

These pentagonal prisms lie on the margin of the polytope at a sharp angle to the 4D viewpoint, so they look somewhat foreshortened. In 4D, of course, they are perfectly uniform.

Centered on a Pentagonal Prism

The above projections show the 5,20-duoprism from a 4D viewpoint that looks edge-on at the ring of icosagonal prisms. Here's another view that looks edge-on at the ring of pentagonal prisms:

Here are the 5 icosagonal prisms:

These icosagonal prisms look quite squished, because they lie at a sharp angle to the 4D viewpoint.

Here are the 8 pentagonal prisms that lie on the near side (facing the 4D viewpoint):

And here are the 10 pentagonal prisms that lie on the far side (facing away from the 4D viewpoint):

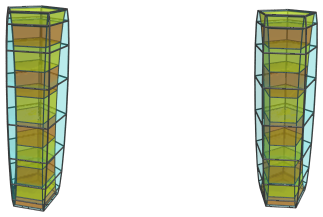
The remaining 2 pentagonal prisms lie on the limb, foreshortened to pentagons:

Coordinates

The Cartesian coordinates of the 5,20-duoprism, centered on the origin and with edge length 2, are:

• (0, ±A, F, 0)
• (±A, 0, F, 0)
• (±B, ±C, F, 0)
• (±C, ±B, F, 0)
• (±D, ±E, F, 0)
• (±E, ±D, F, 0)

• (0, ±A, G, ±φ)
• (±A, 0, G, ±φ)
• (±B, ±C, G, ±φ)
• (±C, ±B, G, ±φ)
• (±D, ±E, G, ±φ)
• (±E, ±D, G, ±φ)

• (0, ±A, H, ±1)
• (±A, 0, H, ±1)
• (±B, ±C, H, ±1)
• (±C, ±B, H, ±1)
• (±D, ±E, H, ±1)
• (±E, ±D, H, ±1)

where:

A	=	2√(2φ2+√(11φ+7))
B	=	√(2+√(φ+2))
C	=	√(6+8φ+√(145φ+90))
D	=	√(4+2φ+√(20φ+15))
E	=	√(4+6φ+√(76φ+47))
F	=	√((10+2√5)/5)
G	=	√((5−√5)/10)
H	=	−√((5+2√5)/5)

and φ=(1+√5)/2 is the Golden Ratio.