The Truncated 5-cell
The truncated 5-cell is a polychoron bounded by 10 cells (5 tetrahedra and 5 truncated tetrahedra), 30 polygons (20 triangles and 10 hexagons), 40 edges, and 20 vertices. It is formed by truncating a pentachoron at one third of its edge length, so that its triangular faces become hexagons. New triangular faces form in place of the original vertices, forming new tetrahedral cells, and the original tetrahedral cells become truncated tetrahedra.
Structure
The following image shows the parallel projection of the truncated 5-cell into 3D:
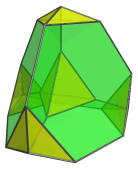
The five tetrahedral cells are rendered in yellow, and are clearly visible here. Four of them appear to be flattened, due to foreshortening. They are regular tetrahedra in 4D.
The following images show where the truncated tetrahedral cells are:
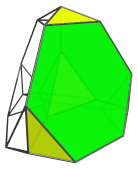
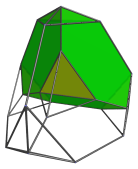
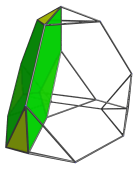
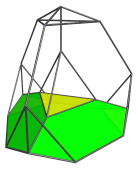
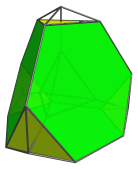
Four of these cells also appear flattened due to foreshortening, but they are uniform truncated tetrahedra in 4D.
Perspective Projection
The following animation shows the perspective projection of the truncated 5-cell rotating in the ZW plane.
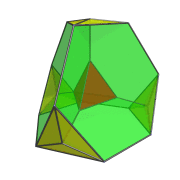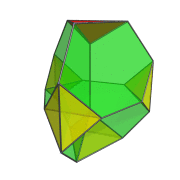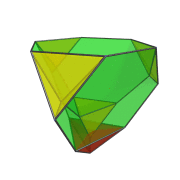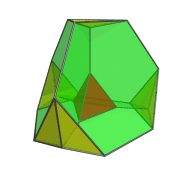
The red tetrahedron and one of the yellow tetrahedra appear to be turning inside-out and engulfing each other, but this is merely an artifact of the perspective projection. In 4D, they neither deform nor touch each other.
Coordinates
The Cartesian coordinates of the truncated 5-cell, centered on the origin and having edge length 2, are:
|
|
Simpler coordinates can be obtained in 5D as all permutations of coordinates of:
- (0, √2, 2√2, 2√2, 2√2)
The 4D coordinates are derived by projecting these 5D coordinates back into 4D using a symmetric projection.




