The Grand Antiprism
The grand antiprism is a uniform polychoron bounded by 320 cells (20 pentagonal antiprisms, 300 tetrahedra), 720 polygons (700 triangles, 20 pentagons), 500 edges, and 100 vertices. It was discovered in 1965 by Conway and Guy.
It is an unusual uniform polychoron that has no Wythoff construction: it cannot be constructed by reflection through a series of mirrors. Its 20 pentagonal antiprisms are arranged into two rings of 10 antiprisms each, interlocking with each other through a toroidal sheet of the 300 tetrahedra. Topologically speaking, its two rings correspond with the two circular tori of the duocylinder, and the sheet of 300 tetrahedra corresponds with the duocylinder's ridge.
Structure
Two Rings
We will explore the grand antiprism by perspective projection. First, we'll start with the two rings of pentagonal antiprisms. The two images below show two views of these two rings:

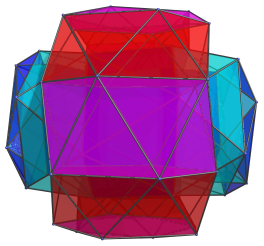
For clarity's sake, we have omitted the tetrahedral cells altogether.
The red and purple ring consists of 10 pentagonal antiprisms, which appear flattened because they lie at an angle to the 4D viewpoint. The blue and cyan tube is actually also a ring of 10 pentagonal antiprisms, but because the ring is seen laterally from the 4D viewpoint, it projects into a tubular volume. We hide the red and purple ring in the next image so that we can see this ring more clearly:

Notice that there is actually an inner tube encased inside the outer tube. The inner tube and the outer tube are actually the two halves of the ring in 4D, joined together by the blue antiprisms on the ends of the tubes. The inner tube is farther away in 4D, so it appears smaller; the outer tube is closer, so it appears bigger. These pentagonal antiprisms actually form a circular ring in 4D, just like the red and purple ring; the flattening into the “tube-within-a-tube” as seen here is merely an artifact of the perspective projection into 3D. In the same way, all the pentagonal antiprisms are identical in 4D, but the ones nearer the ends of the tube appear flattened because of the projection.
Blue Ring Tetrahedra
A sheet of 300 tetrahedra connects these two rings together. They are divided into 200 tetrahedra which share a face with one of the antiprisms, and 100 tetrahedra that only share faces with other tetrahedra. The first group of 200 tetrahedra may be further divided into two groups of 100 each, with the tetrahedra in each group sharing a face with one of the two rings. The image below shows the 100 tetrahedra that share a face with the antiprisms in the blue and cyan ring:

To reduce visual clutter, we will now apply Hidden Surface Removal. The next two images hide the cells that are on the far side of the grand antiprism, showing only those on the side facing the 4D viewpoint.


The second image is the same projection as the first image, but viewed from an angle in order to show that these tetrahedra come in pairs: each tetrahedron joined to one antiprism also shares a face with another tetrahedron joined to the next antiprism in the ring.
Due to the perspective projection, the tetrahedra that are halfway between the near side and the far side are also clipped, so the number of tetrahedra is less than half of the total: only 40 are shown here. The far side of the blue and cyan ring, along with the tetrahedra connected to it, are shown in the next image:

The blue bases of the five tetrahedra in the foreground show where this half of the ring is joined to the first half.
Red Ring Tetrahedra
Since the red and purple ring also lies on the far side of the grand antiprism, we now take a look at the tetrahedra that share a face with the antiprisms in that ring:

In interests of clarity, the tetrahedra that lie on the near side of the grand antiprism have been omitted. Just like the tetrahedra joined to the blue ring, these tetrahedra also come in pairs between adjacent antiprisms in the ring. In fact, the structure of both rings is identical; they only appear differently in projection because they are being seen at different angles.
The next image shows the tetrahedra that lie on the near side of the grand antiprism. Since the red ring pentagonal antiprisms lie just out of view under perspective projection, we only see their outline here.

In-between Tetrahedra
The tips of both sets of tetrahedra, those joined to the red ring and those joined to the blue ring, touch a vertex of the antiprisms in the opposite ring. Either set also shares edges with the other set. However, they do not have common faces between them; instead, another layer of 100 tetrahedra lie between these two layers. We show these last tetrahedra below:


For clarity, we show the tetrahedra lying on the far side (left) and the near side (right) of the grand antiprism separately.
These tetrahedra do not share a face with each other; but they do share edges, forming a sheet sandwiched between the two rings, and straddling the 200 tetrahedra that share a face with the rings. Each of these tetrahedra share an edge with a member of the blue ring and the opposite edge with a member of the red ring.
Putting it Together
Now that we understand the structure of the grand antiprism, we can put the different layers together.
The half of the blue ring on the near side of the grand antiprism lies closest to the 4D viewpoint, so we start with that and successively add the layers of tetrahedra to it until we reach the red ring. Then, to show what happens on the far side of the grand antiprism, we continue by showing the red ring while hiding the near-side cells, and keep going until we reach the far half of the blue ring. The following animation demonstrates this:

In total, we have 10 pentagonal antiprisms in the blue ring and 10 pentagonal antiprisms in the red ring, for a total of 20 pentagonal antiprisms. There are 100 tetrahedra sharing a face with members of the blue ring, 100 tetrahedra sharing a face with members of the red ring, and 100 tetrahedra sharing a face with four of the previous 200 tetrahedra, giving a total of 300 tetrahedra.
Construction
The 300 tetrahedra of the grand antiprism are actually a subset of the 600 tetrahedra of the 600-cell. It can be constructed from the 600-cell by removing two rings of 10 vertices each from the 600-cell's 120 vertices, and then taking the convex hull. These two rings correspond with the two rings of pentagonal antiprisms. Removing these vertices removes two rings of 150 tetrahedra each from the 600-cell, introducing two rings of 10 pentagonal antiprisms each.
Conversely, we can erect pyramids on each of the pentagonal prisms, thus adding 20 vertices to the grand antiprism, and then fill in the remaining gaps with 20 florets of 5 tetrahedra each (10 florets on each ring, fitting between each adjacent pair of pyramids). Since each pyramid consists of 10 tetrahedra each (one per triangular face of the pentagonal prism), and the 20 florets contain a total of 100 tetrahedra, this adds 200+100=300 tetrahedra to the existing 300 tetrahedra of the grand antiprism, turning it into a 600-cell.
Other Views
The following animation shows the grand antiprism rotating in the plane that the blue ring lies in:
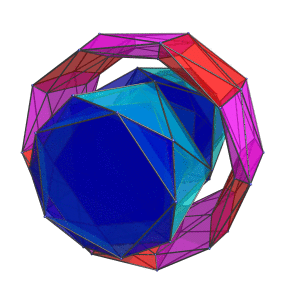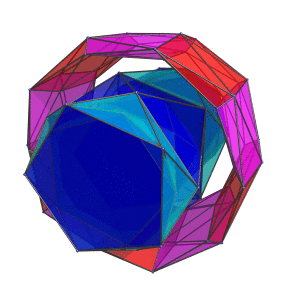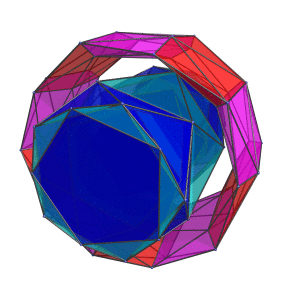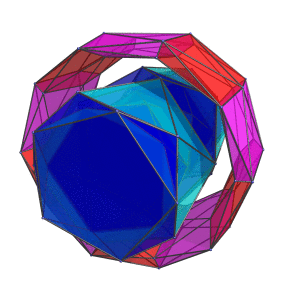
For clarity, the tetrahedral cells are omitted.
Coordinates
Derivation
As we have mentioned above, the grand antiprism can be constructed from the 600-cell by removing two rings of vertices from two complementary planes. We now use that construction to derive coordinates for the grand antiprism.
Recall that the 600-cell's coordinates are all permutations and changes of sign of:
(1,1,1,1)
(2,0,0,0)
along with even permutations and all changes of sign of:
(φ,1,φ−1,0)
where φ=(1+√5)/2 is the Golden Ratio.
In the next sections we will find two rings of vertices to be deleted from this set, and thereby obtain the coordinates for the grand antiprism.
The First Ring to be Removed
We will choose one of the rings to be deleted to include the points (±2,0,0,0) so that the resulting coordinates will have a nice, “upright” orientation, if we consider the grand antiprism to be resting on one of its pentagonal antiprisms. The second ring, then, will lie in the hyperplane orthogonal to (±2,0,0,0); its points will have a zero dot product with (±2,0,0,0). Among the points in this hyperplane are (0,±2,0,0), which we will select for our second ring.
Next, we begin constructing the first ring. Let's start with the point (2,0,0,0). Its immediate neighbours have their first coordinate equal to φ, because they lie in the closest horizontal hyperplane below (2,0,0,0). Therefore, they are:
- (φ, ±1, ±φ−1, 0)
- (φ, ±φ−1, 0, ±1)
- (φ, 0, ±1, ±φ−1)
These are the 12 vertices of an icosahedron in the hyperplane below (2,0,0,0).
Since the two rings must be orthogonal, all vertices that lie on the first ring must have a dot product of zero with vertices in the second ring, including (0,±2,0,0). This means that among the 12 neighbours of (2,0,0,0), the only valid candidates to be a member of the first ring must have a zero dot product with (0,±2,0,0). This reduces the set of candidates for the first ring to:
- (φ, 0, ±1, ±φ−1)
Furthermore, since the two rings are great circles on the 600-cell, if we choose (φ,0,1,φ−1) then (φ,0,−1,−φ−1) will be included as well, since otherwise the ring would not be a great circle, and indeed, will not have 10 vertices. Conversely, if we choose (φ,0,1,−φ−1) then it entails including (φ,0,−1,φ−1). So there are really only two choices. For our purposes, we will pick (φ,0,1,φ−1) to be the second point on the first ring. Thus, our first ring so far consists of:
- (2, 0, 0, 0)
- (φ, 0, 1, φ−1)
The third point must be a neighbour of the second point, must be orthogonal to (0,±2,0,0), and must lie the plane defined by these first two points. The only possibility is:
- (φ−1, 0, φ, 1)
A similar reasoning leads us to the fourth and fifth points:
- (−φ−1, 0, φ, 1)
- (−φ, 0, 1, φ−1)
This gives us half of the first circle. The other half consists of points that are antipodal to the points in the first half, that is:
- (−2, 0, 0, 0)
- (−φ, 0, −1, −φ−1)
- (−φ−1, 0, −φ, −1)
- (φ−1, 0, −φ, −1)
- (φ, 0, −1, −φ−1)
Collecting all these points, we have the vertices for the first ring as:
- (±2, 0, 0, 0)
- (±φ, 0, ±1, ±φ−1)
- (±φ−1, 0, ±φ, ±1)
where there are an even number of negative signs in the last two coordinates. Or, to be unambiguous, the latter two sets of points can be written:
- ±(±φ, 0, 1, φ−1)
- ±(±φ−1, 0, φ, 1)
with the understanding that we take all combinations of signs where indicated by the ±.
The Second Ring to be Removed
Now we come to the second ring. We have already picked our first point, (0,2,0,0). Its 12 neighbours are:
- (0, φ, ±φ−1, ±1)
- (±φ−1, φ, ±1, 0)
- (±1, φ, 0, ±φ−1)
Since vertices in the second ring must have a zero dot product with all vertices in the first ring, this immediately narrows them down to:
- (0, φ, −φ−1, 1)
- (0, φ, φ−1, −1)
Tracing out the subsequent points in the second ring in the same way we did for the first ring, we obtain its vertices as:
- (0, ±2, 0, 0)
- ±(0, ±φ, φ−1, −1)
- ±(0, ±φ−1, 1, −φ)
There are an odd number of negative signs in the last two coordinates of the second and third rows.
It is left as an exercise for the reader to verify that these coordinates indeed do have a zero dot product with all the coordinates from the first ring.
Removing Two Rings from the 600-cell
Putting the vertices from the two rings together, the 20 vertices to be removed from the 600-cell are:
|
|
The vertices left after removing them from the 600-cell are:
- ±(±φ, 0, 1, −φ−1)
- ±(±φ−1, 0, φ, −1)
- ±(0, ±φ, φ−1, 1)
- ±(0, ±φ−1, 1, φ)
along with all changes of sign of:
|
|
These are the coordinates of the grand antiprism.




