The Truncated 120-cell

---

The truncated 120-cell is a uniform polychoron bounded by 720 cells (120 truncated dodecahedra, 600 tetrahedra), 3120 polygons (2400 triangles, 720 decagons), 4800 edges, and 2400 vertices.

It is a relatively simple member of the 120-cell/600-cell family of uniform polytopes, and, as its name implies, can be constructed by truncating the 600 vertices of the 120-cell. Equivalently, it can be constructed by expanding the edges of the 120-cell outwards radially, and filling in the resulting gaps with 600 tetrahedra.

Structure

The Near Side

First Layer

As is customary, we shall explore the structure of the truncated 120-cell by means of its parallel projection into 3D.

The above image shows the nearest truncated dodecahedron to the 4D viewpoint. For clarity, we have omitted edges and vertices not on this nearest cell, and render all the other cells in a transparent color.

The 20 triangular faces of this nearest truncated dodecahedron are joined to 20 tetrahedra, shown in red below:

Second Layer

The 12 decagonal faces of the nearest cell are joined to another 12 truncated dodecahedra:

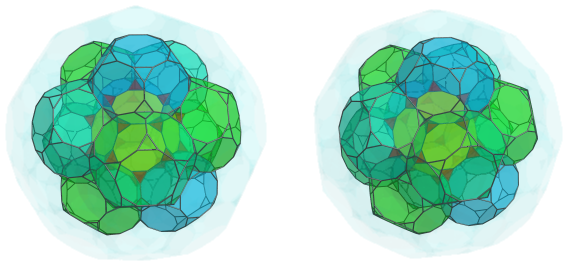
Nestled among these truncated dodecahedra are 20 more tetrahedra, joined to the previous 20 tetrahedra by an edge:

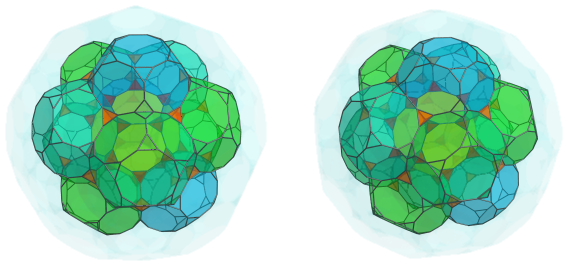
Slightly farther out from them are another 30 tetrahedra, straddling each adjacent pair of truncated dodecahedra:

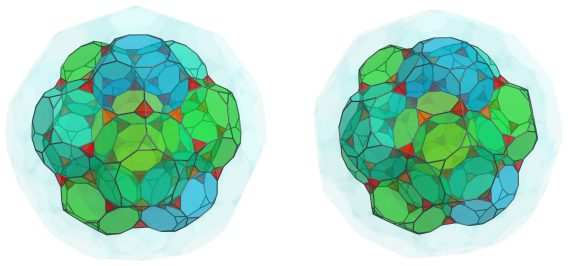
The remaining exposed triangular faces of the truncated dodecahedra are joined to another 60 tetrahedra, which come in circles of 5:

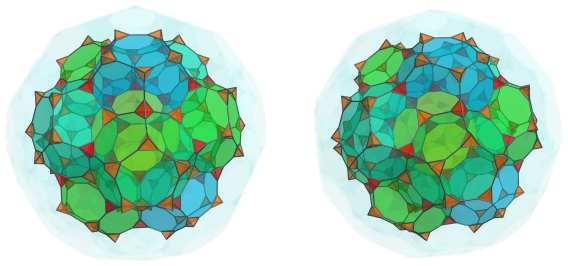
Third Layer

Over these tetrahedra are a third layer of 20 truncated dodecahedra:

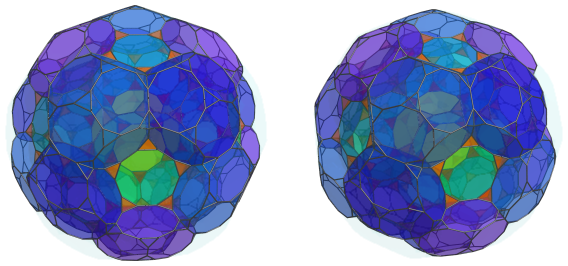
Between each adjacent pair of truncated dodecahedra are more pairs of tetrahedra, adding another 60 tetrahedra:

The remaining exposed decagonal faces of the previous layer of truncated dodecahedra are where another 12 truncated dodecahedra are joined:

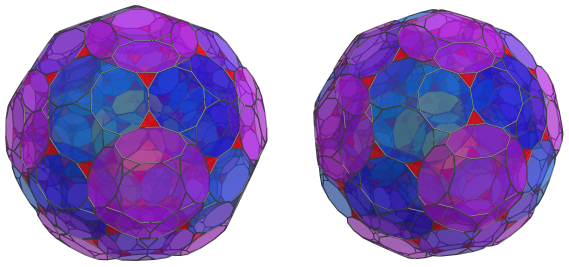
Another 60 tetrahedra straddle these 12 truncated dodecahedra and the previous 20 truncated dodecahedra:

Finally, the remaining exposed triangular faces of those 20 truncated dodecahedra are peaked by 20 more tetrahedra:

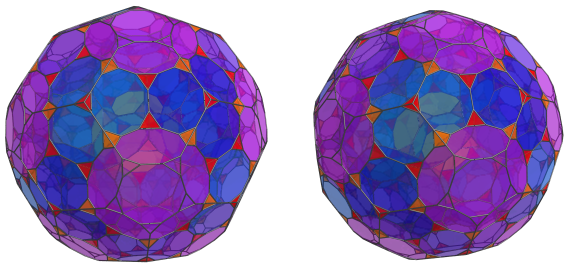
These are all the cells on the near side of the truncated 120-cell.

The Equator

Next comes the cells that lie on the equator of the truncated 120-cell. There are 30 truncated dodecahedra that lie on the equator:

For the sake of clarity, we've omitted the cells that were previously seen.

There are 60 tetrahedra that lie on the equator:

These are all the cells that lie on the equator. The remaining 12 decagonal gaps do not correspond to any equatorial cells; they are where 12 truncated dodecahedra on the near side of the polytope touches their corresponding counterparts on the far side.

Past this point, we reach the far side of the truncated 120-cell, where the arrangement of cells exactly mirrors the arrangement of cells on the near side, as described earlier.

Summary

The following table summarizes the cell counts in the truncated 120-cell:

Region	Layer
Near side	1	1	20
	2	12	20 + 30 + 60 = 110
	3	20 + 12 = 32	60 + 60 + 20 = 140
	Subtotal	45	270
Equator		30	60
Far side	3	32	140
	2	12	110
	1	1	20
	Subtotal	45	270
Grand total		120	600

Coordinates

The coordinates of the truncated 120-cell, centered on the origin and having edge length 2, are all permutations of coordinate and changes of sign of:

• (1, 3+4φ, 3+4φ, 3+4φ)
• (φ³, φ³, φ³, 5+6φ)
• (2φ², 2φ², 2φ², 2φ⁴)

as well as even permutations of coordinate and all changes of sign of:

(0, 1, 4+5φ, φ5) (0, 1, 4+7φ, 1+3φ) (0, φ2, 3φ3, 2+5φ) (0, φ2, 5+6φ, φ4) (0, 2φ, 2φ4, 2φ3) (1, φ2, 4+7φ, 2φ2) (1, φ3, 3φ3, 3+4φ)

(φ2, 2φ, 4+7φ, φ3) (φ2, 2φ2, 4+5φ, 3+4φ) (φ2, 2φ3, 2+5φ, 3+4φ) (2φ, φ4, φ5, 3+4φ) (φ3, 2φ2, φ5, 2+5φ) (φ3, 1+3φ, 4+5φ, 2φ3) (2φ2, 1+3φ, 3φ3, φ4)

where φ=(1+√5)/2 is the Golden Ratio.