The Joined 120-cell

---

The joined 120-cell is a Catalan polychoron bounded by 720 pentagonal bipyramids, 3600 isosceles triangles, 3600 edges (1200 short, 2400 long), and 720 vertices. It is the dual of the rectified 600-cell.

The cells are pentagonal bipyramids with isosceles triangular faces with an edge length ratio of 3−φ : 2, or approximately 0.691 : 1, where φ=(1+√5)/2 is the Golden Ratio. They are duals of the uniform pentagonal prism.

Joined in the name refers to the join operator in Conway's polyhedron notation (suitably generalized to 4D), which can be applied to the 120-cell to obtain this polytope.

Structure

We will explore the structure of the joined 120-cell using its parallel projections into 3D.

First Layer

In the following images, we show the 12 pentagonal bipyramidal cells that surround the vertex closest to the 4D viewpoint:

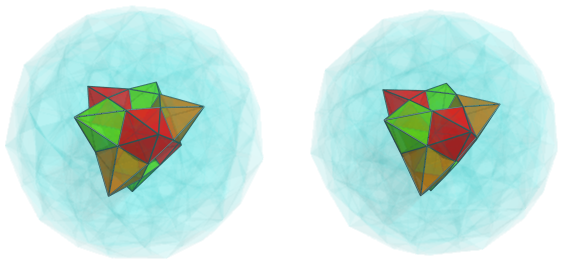
As can be seen, these cells are laid out in a dodecahedral pattern, corresponding with the faces of a dodecahedron and the vertices of an icosahedron.

Second Layer

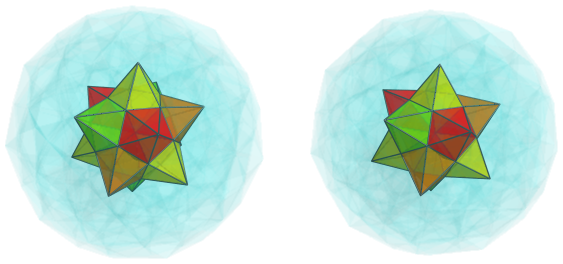
Straddling the previous cells are another 30 cells, corresponding with the edges of an icosahedron:

Third Layer

Surrounding the previous cells are another layer of 60 cells:

Fourth Layer

Another 42 cells fit into the visible depressions formed by the previous cells. Twelve of them correspond with the vertices of an icosahedron:

These cells touch the vertices at the tip of the first layer cells.

The other 30 of them correspond with the edges of an icosahedron, and only touch the 2nd and 3rd layer cells:

Fifth Layer

The new gaps visible are filled in by another 60 cells:

Sixth Layer

Another 60 cells fit between the shallow ridges of the previous cells, tracing out the outline in the shape of a truncated dodecahedron:

These cells are near the equator of the polytope, and so appear more distorted due to foreshortening. In 4D, of course, they are undistorted.

Seventh Layer

In the remaining areas with exposed faces from the 5th layer cells lie another 60 cells, in star-shaped florets of 5 cells each:

These are all the cells that lie on the near side of the polychoron, facing the 4D viewpoint. Past this point, we come to the limb of the polytope, or the equator.

The Equator

There are 12 axial cells in the equator of the polychoron that correspond with the vertical of an icosahedron:

For clarity, we have omitted the cells on the near side of the polytope that we saw earlier.

These cells have been foreshortened into pentagons because they lie at a 90° angle to the 4D viewpoint. They are, of course, full-bodied pentagonal bipyramids in 4D.

Between these cells are 60 other cells in oblique orientation, shown below:

The remaining gaps on the limb of the polytope do not correspond to any cells; they are where the 7th layer cells share a face with their corresponding counterparts on the far side of the polytope.

Past the equator, the 7 layers of cells we saw on the near side of the polychoron repeat in reverse order, forming the far side of the polytope.

Summary

The following table summarizes the cell counts on each layer of the joined 120-cell:

Region	Layer
Near side	1	12
	2	30
	3	60
	4	12 + 30 = 42
	5	60
	6	60
	7	60
	Subtotal	324
Equator		12 + 60 = 72
Far side	7	60
	6	60
	5	60
	4	12 + 30 = 42
	3	60
	2	30
	1	12
	Subtotal	324
Grand total		720

Coordinates

The Cartesian coordinates of the joined 120-cell are all permutations of coordinates and changes of sign of:

• (0, 0, 0, 4)
• (0, 0, 6−2φ, 6−2φ)
• (7−4φ, −1+2φ, −1+2φ, −1+2φ)
• (−4+3φ, −4+3φ, −4+3φ, 2+φ)
• (3−φ, 3−φ, 3−φ, 5/φ)
• (2, 2, 2, 2)

as well as even permutations of coordinates and all changes of sign of:

• (0, 7−4φ, 2+φ, 3−φ)
• (0, −4+3φ, 5/φ, −1+2φ)
• (0, 2/φ, 2, 2φ)
• (−4+3φ, 3−φ, 6−2φ, −1+2φ)

where φ=(1+√5)/2 is the Golden Ratio.

These coordinates correspond with a dual rectified 600-cell of edge length 3φ−4.