The Joined 16-cell

---

The joined 16-cell is a Catalan polychoron bounded by 32 triangular bipyramids, 96 isosceles triangles, 88 edges (24 long, 64 short), and 24 vertices. It is the dual of the rectified tesseract.

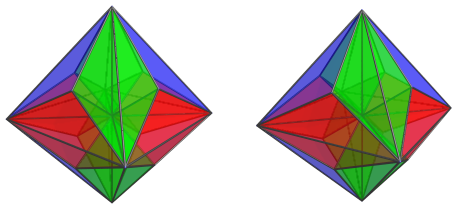
As a Catalan polychoron, it is cell-transitive. Each cell is a triangular bipyramid having triangular symmetry around its axis.

The faces are congruent isosceles triangles, having two kinds of edges: short edges, shown in blue above, and long edges, shown in red. The ratio of edge lengths is √7 : 3√2, or approximately 0.624 : 1. Hence, the short edges are slightly shorter than those found in the dual of the uniform triangular prism, which is also a triangular bipyramid except of slightly different proportions.

Each long edge has 4 incident cells that meet at it, whereas each short edge has 3 incident cells.

There are two kinds of vertices: 8 apical vertices, corresponding to the vertices of a tesseract, and 16 angular vertices, corresponding to the vertices of a 16-cell, making a total of 24 vertices.

The parallel projection of the joined 16-cell into 3D, centered on an apical vertex, is an octahedron.

Structure

The Near Side

We shall explore the structure of the joined 16-cell using its parallel projections into 3D, centered on one of its apical vertices.

The following image shows this nearest vertex to the 4D viewpoint:

For the sake of clarity, we render all the other elements of the polytope in a light transparent color.

Surrounding this vertex are 12 cells, which we can group into 3 rings of four each.

The next images show the first of these rings:

These cells appear distorted from their symmetrical proportions because they lie at a rather steep angle to the 4D viewpoint. This is a foreshortening side-effect of the projection into 3D. In 4D, they have perfect trigonal symmetry.

The next image shows all 4 cells together:

The next images show the cells from the second ring:

The following images the cells from the third ring:

Here are all 3 rings together:

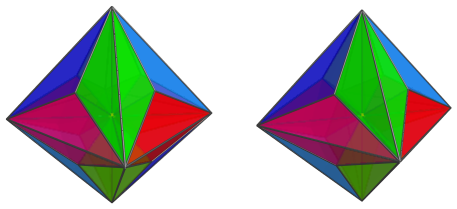
These 12 cells lie on the near side of the polychoron. Next, we come to the cells on the limb, or equator, of the projection.

The Equator

At the equator of the joined 16-cell, are 8 cells that lie at a 90° angle from the 4D viewpoint. The following image shows two of these cells:

For clarity, we omit the cells on the near side of the polychoron that we saw earlier.

These two cells have been foreshortened into triangles, because they lie at a 90° angle to the 4D viewpoint. This foreshortening is along the axis symmetry, unlike the foreshortening we saw on the near side cells, which was along an oblique direction.

The following images show the rest of the equatorial cells:

Summary

Past this point, the layout of cells on the far side of the polytope mirror the structure of the cells on the near side.

Thus in total, there are 12 cells on the near side, 8 cells on the equator, and 12 cells on the far side, for a total of 32 cells.

Coordinates

The Cartesian coordinates of the joined 16-cell are all permutations of coordinate and changes of sign of:

• (0, 0, 0, 3)
• (1, 1, 1, 1)

These coordinates correspond with a dual rectified tesseract of edge length √2/3.