The Rhombipyramidal Hecatonenneacontadichoron
The rhombipyramidal hecatonenneacontadichoron is a Catalan polychoron bounded by 192 skew rhombic pyramids, 480 polygons (96 kites, 192 small triangles, 192 large triangles), 368 edges (64 very short, 96 short, 96 medium, 48 long, 64 very long), and 80 vertices. It is the dual of the runcitruncated tesseract.

As a Catalan polychoron, it is cell-transitive. Each cell is a skew rhombic pyramid with bilateral symmetry. The following animation shows one such cell
The base of this skew pyramid is a kite, a quadrilateral with bilateral symmetry. The other 4 faces consist of a pair of smaller triangles and a pair of larger triangles. There are 5 types of edges altogether. The following table lists each edge type, its corresponding color in the above image, its relative length to the longest edge (type E), and its total number in the entire polytope.
| Type | Color | Length | Count | |
|---|---|---|---|---|
| A | red | (13−2√2)/23 | 0.442 | 64 |
| B | brown | (2/1127)√(70186+18628√2) | 0.551 | 96 |
| C | green | √(1439−188√2)/49 | 0.699 | 96 |
| D | magenta | (2/49)√(246+93√2) | 0.793 | 48 |
| E | blue | 1 | 1 | 64 |
| Total count | 368 | |||
Thus, the kite base has edges BBDD, the small triangles have edges ABC, and the large triangles have edges CDE. There are 96 kites altogether, 192 small triangles (ABC), and 192 large triangles (CDE), for a total of 480 polygons.
The following image shows the edge structure of the polychoron, using the above coloring scheme:

The projection envelope of the rhombipyramidal hecatonenneacontadichoron is a deltoidal icositetrahedron, one of the Catalan solids, albeit not of the exact proportions.
Structure
We will explore the structure of the rhombipyramidal hecatonenneacontadichoron using its parallel projections into 3D, centered on an order-14 vertex.
The Near Side
The following image shows the nearest vertex to the 4D viewpoint:

For clarity, we render the rest of the polytope in a light transparent color.
The First Layer
Surrounding this nearet vertex are 24 cells, shown below:






The Second Layer
Touching these cells are a second layer of 48 cells, shown next:



The Third Layer
Straddling these cells are another 24 cells:

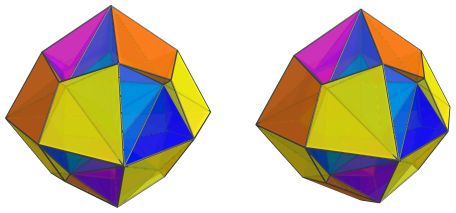

These cells lie at a steep angle of about 79° to the 4D viewpoint; because of this, they appear here foreshortened to rather flat shapes. In 4D, of course, they are the same as the other cells we have seen.
These are all the cells that lie on the near side of the polytope: the side facing the 4D viewpoint.
The Far Side
Past this point, we come to the far side of the polytope, where the cells face away from the 4D viewpoint. The layout of cells on the far side is identical to the near side, except in reverse order, perfectly mirroring the cells on the near side.
Summary
Thus, the following table summarizes the cell counts in each layer of the polychoron:
| Region | Layer | Cells |
|---|---|---|
| Near side | 1 | 24 |
| 2 | 48 | |
| 3 | 24 | |
| Subtotal | 96 | |
| Far side | 3 | 24 |
| 2 | 48 | |
| 1 | 24 | |
| Subtotal | 96 | |
| Grand total | 192 | |
Coordinates
The Cartesian coordinates of the rhombipyramidal hecatonenneacontadichoron are all permutations of coordinate and changes of sign of:
- (0, 0, 0, (3+√2)/7)
- (0, 0, (4+√2)/14, (4+√2)/14)
- (0, (5+√2)/23, (5+√2)/23, (5+√2)/23)
- (1/4, 1/4, 1/4, 1/4)
These coordinates correspond with a dual runcinated tesseract of edge length 2(√2−1).




