The Bidecachoron

---

The bidecachoron is a Catalan polychoron bounded by 30 tetragonal disphenoids, 60 isosceles triangles, 40 edges (20 short, 20 long), and 10 vertices. It is the dual of the bitruncated 5-cell. Like its dual, the bidecachoron also has a higher degree of symmetry than the 5-cell itself.

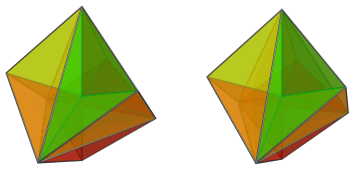
Its cells are tetragonal disphenoids with 4 short edges lacing 2 opposite long edges. The following image shows one of them:

The two long edges at the top and bottom of the cell are shown in red, while the 4 short edges lacing them are in blue. The ratio of short to long edge lengths is √3 : √5 (approximately 0.775 : 1). Due to this length disparity, the cell is somewhat flat compared to a regular tetrahedron. However, all 4 faces are congruent isosceles triangles, each with 2 short edges and 1 long edge.

Structure

We will explore the structure of the bidecachoron using its parallel projections into 3D.

The Near Side

The following image shows the vertex nearest to the 4D viewpoint. It shows up as a point in the middle of the projection:

For clarity, we have omitted other edges and vertex, and render cells in a light transparent color.

The projection envelope of this vertex-first projection is a cube. There are 12 cells that surround the central vertex. They come in 6 pairs corresponding with the faces of this cube. The images below show each of these pairs:

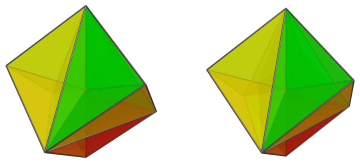
The triangular face shared between each pair corresponds to an edge of a tetrahedron inscribed in the cube; thus opposite pairs have opposite orientation.

The Equator

Next, we come to the limb, or the equator, of the polychoron. There are 6 cells here, corresponding with the faces of the cubical projection envelope.

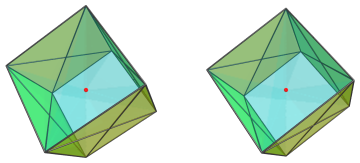
For clarity, we have omitted the near side cells we saw earlier.

These cells have been foreshortened into squares, because they lie at a 90° angle to the 4D viewpoint. In 4D space, of course, they are full-bodied tetragonal disphenoids, identical to the other cells we have seen.

In this projection the long edges lie on the diagonals of the square faces of the cubical projection envelope, while the short edges lie on the edges of the cube.

The Far Side

The cells on the far side have exactly the same arrangement as the cells on the near side, except with opposite orientation. There are 12 such cells, and they all surrounded the farthest vertex from the 4D viewpoint, the antipodal vertex to the nearest one. The following image shows this farthest vertex:

The next set of images show each of the 6 pair of cells surrounding this farthest vertex:

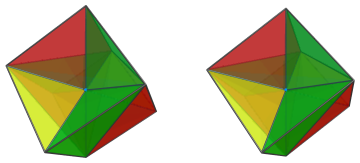
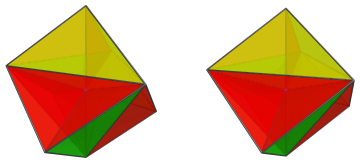
These are all the cells that lie on the far side of the polytope.

Summary

In total, the near side and far side of the polytope each have 12 cells, so along with the 6 equatorial cells we have a total of 12 + 6 + 12 = 30 cells.

Coordinates

The Cartesian coordinates of the bidecachoron are:

• ±(1/√10, 1/√6, 1/√3, ±1)
• ±(1/√10, 1/√6, −2/√3, 0)
• ±(1/√10, −3/√6, 0, 0)
• (±4/√10, 0, 0, 0)

These coordinates correspond with a dual bitruncated 5-cell of edge length 1.