The Gyroelongated Pentagonal Cupolarotunda

---

The gyroelongated pentagonal cupolarotunda is the 47th Johnson solid (J47). It has 35 vertices, 80 edges, and 47 faces (35 equilateral triangles, 5 squares, and 7 pentagons).

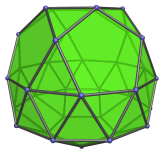
The gyroelongated pentagonal cupolarotunda can be constructed by attaching a pentagonal rotunda and a pentagonal cupola to a decagonal antiprism, or equivalently, adding a pentagonal rotunda to a gyroelongated pentagonal cupola (J24), or adding a pentagonal cupola to a gyroelongated pentagonal rotunda (J25).

J47 is one of the few Johnson solids that are chiral; it is distinct from its own mirror image:

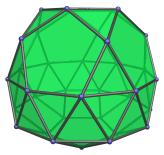
Projections

Here are some views of the gyroelongated pentagonal cupolarotunda from various angles:

Projection	Description
	Top view.
	Front view.
	Side view.
	9° side view.

Coordinates

The Cartesian coordinates of the gyroelongated pentagonal cupolarotunda with edge length 2 are:

• (0, −√((10+2√5)/5), H+√((20+8√5)/5))
• (±1, √((5+2√5)/5), H+√((20+8√5)/5))
• (±φ, −√((5−√5)/10), H+√((20+8√5)/5))
• (0, √((20+8√5)/5), H+√((10+2√5)/5))
• (±φ, −√((25+11√5)/10), H+√((10+2√5)/5))
• (±φ², √((5+√5)/10), H+√((10+2√5)/5))
• (±1, ±√(3+4φ), H)
• (±φ², ±√(2+φ), H)
• (±2φ, 0, H)
• (0, ±2φ, −H)
• (±√(3+4φ), ±1, −H)
• (±√(2+φ), ±φ², −H)
• (√((10+2√5)/5), 0, −(H + 2√((3−φ)/5)))
• (√((5−√5)/10), ±φ, −(H + 2√((3−φ)/5)))
• (−√((5+2√5)/5), ±1, −(H + 2√((3−φ)/5)))

where H = √(√(11φ+7)−2φ−1), approximately 0.862397, is half the height of a decagonal antiprism of edge length 2, and φ = (1+√5)/2 is the Golden Ratio.