The Sphenocorona
The sphenocorona is the 86th Johnson solid (J86). Its surface consists of 12 equilateral triangles and 2 squares, for a total of 14 faces, 22 edges, and 10 vertices.
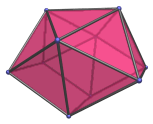
The sphenocorona is one of the special Johnson solids at the end of Norman Johnson's list that are not directly derived from the uniform polyhedra by cut-and-paste operations.
The sphenocorona can be augmented with a square pyramid to form the augmented sphenocorona (J87).
Projections
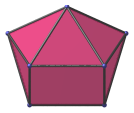
Here are some views of the sphenocorona from various angles:
| Projection | Envelope | Description |
|---|---|---|
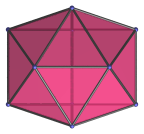 |
Hexagon | Top view. |
 |
Pentagon | Side view. |
 |
Pentagon | Front view. Square faces project to bottom two edges. |
 |
Hexagon | 45° side view. |
Coordinates
The Cartesian coordinates of the sphenocorona with edge length 2 are:
- (0, 0, ±1)
- (±A, √B, ±1)
- (0, √C, ±D)
- (±1, √E, 0)
where A, B, C, D, and E are roots of the following polynomials within the given ranges:
| 15A4 − 24A3 − 100A2 + 112A + 92 = 0, | 1≤A≤2 |
| 225B4 − 24B3 − 3176B2 − 96B + 3600 = 0, | 1≤B≤2 |
| 225C4 − 24C3 − 3176C2 − 96C + 3600 = 0, | 3≤C≤4 |
| 15D4 − 36D3 − 82D2 + 100D + 95 = 0, | 1≤D≤2 |
| E2 − 4E − 20 = 0 | 6≤E≤7 |
Note that B and C are different roots of the same polynomial. E has the closed-form expression 2+2√6.
The approximate numerical values are:
- A = 1.705453885692834
- √B = 1.044713857367277
- √C = 1.914399800381786
- D = 1.578855253321743
- √E = 2.626590848527109




