The Augmented Sphenocorona

---

The augmented sphenocorona is the 87th Johnson solid (J87). Its surface consists of 16 equilateral triangles and 1 square, for a total of 17 faces, 26 edges, and 11 vertices.

It is constructed by augmenting one of the square faces of the sphenocorona (J86) with a square pyramid. The triangular face of the augment that touches the remaining square face is very nearly coplanar: their dihedral angle is approximately 171.8°.

Projections

Here are some views of the augmented sphenocorona from various angles:

Projection	Description
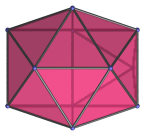	Top view.
	Side view.
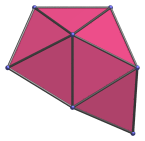	Front view.
	45° side view.
	Parallel to line from augment apex to upper left vertex.

Coordinates

The Cartesian coordinates of the augmented sphenocorona with edge length 2 are:

• (0, 0, ±1)
• (±A, √B, ±1)
• (0, √C, ±D)
• (±1, √E, 0)
• ((A+B√2)/2, (B−A√2)/2, 0)

where A, B, C, D, and E are roots of the following polynomials within the given ranges:

15A4 − 24A3 − 100A2 + 112A + 92 = 0,	1≤A≤2
225B4 − 24B3 − 3176B2 − 96B + 3600 = 0,	1≤B≤2
225C4 − 24C3 − 3176C2 − 96C + 3600 = 0,	3≤C≤4
15D4 − 36D3 − 82D2 + 100D + 95 = 0,	1≤D≤2
E2 − 4E − 20 = 0	6≤E≤7

Note that B and C are different roots of the same polynomial. E has the closed-form expression 2+2√6.

The approximate numerical values are:

• A = 1.705453885692834
• √B = 1.044713857367277
• √C = 1.914399800381786
• D = 1.578855253321743
• √E = 2.626590848527109